题目内容
已知F1、F2是椭圆
+
=1的左、右焦点,O为坐标原点,点P(-1,
)在椭圆上,线段PF2与y轴的交点M满足
+
=
;
(1)求椭圆的标准方程;
(2)⊙O是以F1F2为直径的圆,一直线l:y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.当
•
=λ且满足
≤λ≤
时,求△AOB面积S的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PM |
| F2M |
| 0 |
(1)求椭圆的标准方程;
(2)⊙O是以F1F2为直径的圆,一直线l:y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.当
| OA |
| OB |
| 2 |
| 3 |
| 3 |
| 4 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆的标准方程.
(Ⅱ)由圆O与直线l相切,和m2=k2+1,由
,得(1+2k2)x2+4kmx+2m2-2=0,由此能求出△AOB面积S的取值范围.
|
(Ⅱ)由圆O与直线l相切,和m2=k2+1,由
|
解答:
解:(Ⅰ)∵
+
=
,∴点M是线段PF2的中点,
∴OM是△PF1F2的中位线,
又OM⊥F1F2∴PF1⊥F1F2
∴
,解得a2=2,b2=1,c2=1,
∴椭圆的标准方程为
+y2=1.(5分)
(Ⅱ)∵圆O与直线l相切,∴
=1,即m2=k2+1,
由
,消去y:(1+2k2)x2+4kmx+2m2-2=0,
∵直线l与椭圆交于两个不同点,
∴△>0,∴k2>0,设A(x1,y1),B(x2,y2),
则x1+x2=-
,x1x2=
,
y1y2=(kx1+m)(kx2+m)
=k2x1x2+km(x1+x2)+m2
=
,
•
=x1x2+y1y2=
=λ,
∴
≤λ≤
,∴
≤
≤
,解得:
≤k2≤1,(8分)
S=S△AOB=
|AB|•1
=
•
=
,
设μ=k4+k2,则
≤μ≤2,
S=
,μ∈[
,2],
∵S关于μ在[
,2]上单调递增,
S(
)=
,S(2)=
.
∴
≤S≤
.(13分)
| PM |
| F2M |
| 0 |
∴OM是△PF1F2的中位线,
又OM⊥F1F2∴PF1⊥F1F2
∴
|
∴椭圆的标准方程为
| x2 |
| 2 |
(Ⅱ)∵圆O与直线l相切,∴
| |m| | ||
|
由
|
∵直线l与椭圆交于两个不同点,
∴△>0,∴k2>0,设A(x1,y1),B(x2,y2),
则x1+x2=-
| 4km |
| 1+2 k2 |
| 2m2-2 |
| 1+2k2 |
y1y2=(kx1+m)(kx2+m)
=k2x1x2+km(x1+x2)+m2
=
| m2-2k2 |
| 1+2k2 |
| OA |
| OB |
| 1+k2 |
| 1+2k2 |
∴
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1+k2 |
| 1+2k2 |
| 3 |
| 4 |
| 1 |
| 2 |
S=S△AOB=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1+k2 |
(-
|
=
|
设μ=k4+k2,则
| 3 |
| 4 |
S=
|
| 3 |
| 4 |
∵S关于μ在[
| 3 |
| 4 |
S(
| 3 |
| 4 |
| ||
| 4 |
| 2 |
| 3 |
∴
| ||
| 4 |
| 2 |
| 3 |
点评:本题考查椭圆方程的求法,考查三角形面积的取值范围的求法,解题时要认真审题,注意椭圆弦长公式的合理运用.

练习册系列答案
相关题目
在△ABC中,若a=
,b=
,A=60°,则B=( )
| 3 |
| 2 |
| A、30° | B、45° |
| C、90° | D、120° |
已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连结DM,则DM与平面PAC所成角的大小是( )
| A、30° | B、45° |
| C、60° | D、90° |
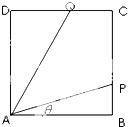 经英国相关机构判断,MH370在南印度洋海域消失.中国两舰艇随即在边长为100海里的某正方形ABCD(如图)海域内展开搜索.两艘搜救船在A处同时出发,沿直线AP、AQ向前联合搜索,且∠PAQ=
经英国相关机构判断,MH370在南印度洋海域消失.中国两舰艇随即在边长为100海里的某正方形ABCD(如图)海域内展开搜索.两艘搜救船在A处同时出发,沿直线AP、AQ向前联合搜索,且∠PAQ=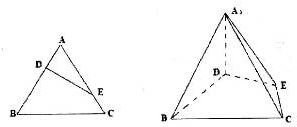 已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足
已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足