题目内容
设有两个命题,命题p:?x∈(1,
)使函数g(x)=log2(ax2+2x-2)有意义;命题q:已知函数f(x)=mx3+nx2的图象在点(-1,2)处的切线恰好与直线2x+y=1平行,且f(x)在[a,a+1]上单调递减.若命题p或q为真,求实数a的取值范围.
| 5 |
| 2 |
考点:复合命题的真假
专题:函数的性质及应用,简易逻辑
分析:对于命题p:?x∈(1,
)使函数g(x)=log2(ax2+2x-2)有意义?不等式ax2+2x-2>0有属于(1,
)的解?a>(
-
)min,x∈(1,
).
利用二次函数的单调性即可得出其最小值.对于命题q:由函数f(x)=mx3+nx2的图象在点(-1,2)处的切线恰好与直线2x+y=1平行,可得
,即可解得m,n.令f′(x)≤0,解得-
≤x≤0.由于f(x)在[a,a+1]上单调递减.可得[a,a+1]⊆[-
,0].即可解得a的取值范围.由命题p或q为真,其中至少有一个为真命题即可得出.
| 5 |
| 2 |
| 5 |
| 2 |
| 2 |
| x2 |
| 2 |
| x |
| 5 |
| 2 |
利用二次函数的单调性即可得出其最小值.对于命题q:由函数f(x)=mx3+nx2的图象在点(-1,2)处的切线恰好与直线2x+y=1平行,可得
|
| 4 |
| 3 |
| 4 |
| 3 |
解答:
解:对于命题p:?x∈(1,
)使函数g(x)=log2(ax2+2x-2)有意义,
则不等式ax2+2x-2>0有属于(1,
)的解;
即a>(
-
)min,x∈(1,
).
∵1<x<
,∴
<
<1,
∴
-
=2(
-
)2-
∈[-
,0).
∴a>-
.
命题q:由f′(x)=3mx2+2nx,
∵函数f(x)=mx3+nx2的图象在点(-1,2)处的切线恰好与直线2x+y=1平行,
∴
,解得m=2,n=4.
∴f(x)=2x3+4x2,f′(x)=6x2+8x,令f′(x)≤0,解得-
≤x≤0.
∵f(x)在[a,a+1]上单调递减.
∴[a,a+1]⊆[-
,0].
∴
,解得-
≤a≤-1.
若命题p或q为真,则-
≤a≤-1或a>-
.
∴实数a的取值范围是[-
,-1]∪(-
,+∞).
| 5 |
| 2 |
则不等式ax2+2x-2>0有属于(1,
| 5 |
| 2 |
即a>(
| 2 |
| x2 |
| 2 |
| x |
| 5 |
| 2 |
∵1<x<
| 5 |
| 2 |
| 2 |
| 5 |
| 1 |
| x |
∴
| 2 |
| x2 |
| 2 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a>-
| 1 |
| 2 |
命题q:由f′(x)=3mx2+2nx,
∵函数f(x)=mx3+nx2的图象在点(-1,2)处的切线恰好与直线2x+y=1平行,
∴
|
∴f(x)=2x3+4x2,f′(x)=6x2+8x,令f′(x)≤0,解得-
| 4 |
| 3 |
∵f(x)在[a,a+1]上单调递减.
∴[a,a+1]⊆[-
| 4 |
| 3 |
∴
|
| 4 |
| 3 |
若命题p或q为真,则-
| 4 |
| 3 |
| 1 |
| 2 |
∴实数a的取值范围是[-
| 4 |
| 3 |
| 1 |
| 2 |
点评:本题考查了存在性问题的等价转化方法、二次函数的单调性、利用研究函数的单调性、导数的几何意义等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
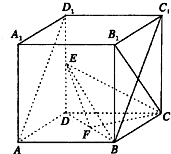 如图所示,在棱长为1的正方体AC1中,E,F分别为DD1,DB的中点.
如图所示,在棱长为1的正方体AC1中,E,F分别为DD1,DB的中点.