题目内容
过双曲线
-
=1的一个焦点作x轴的垂线,求垂线与双曲线的交点到两焦点的距离.
| x2 |
| 144 |
| y2 |
| 25 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:本题可以先求出参数a、b、c和焦点坐标,作出垂线后,求出交点坐标,得到交点到一个焦点的距离,再利用椭圆的定义,求出交点到另一焦点的距离,得到本题结论.
解答:
解:∵双曲线方程为:
-
=1,
∴实半轴长记为a,虚半轴长为b,半焦距为c,
则a2=144,b2=25,c2=a2+b2=144+25=169,
∴a=12,b=5,c=13.
∴焦点F1(13,0),F2(13,0).
过点F2作直线l垂直于x轴,交双曲线于点A,B.
由
,得到yA=
,
∴AF2=
.
由双曲线定义得到:AF1-AF2=2a,
∴AF1=24+
=
.
∴交点到两焦点的距离分别为:
,
.
| x2 |
| 144 |
| y2 |
| 25 |
∴实半轴长记为a,虚半轴长为b,半焦距为c,
则a2=144,b2=25,c2=a2+b2=144+25=169,
∴a=12,b=5,c=13.
∴焦点F1(13,0),F2(13,0).
过点F2作直线l垂直于x轴,交双曲线于点A,B.
由
|
| 25 |
| 12 |
∴AF2=
| 25 |
| 12 |
由双曲线定义得到:AF1-AF2=2a,
∴AF1=24+
| 25 |
| 12 |
| 313 |
| 12 |
∴交点到两焦点的距离分别为:
| 25 |
| 12 |
| 313 |
| 12 |
点评:本题考查了椭圆的定义和方程,本题难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x),g(x)对应值如下表,若f(g(a))≤a,则a的解集为( )
| x | 0 | 1 | -1 |
| f(x) | 1 | 0 | -1 |
| G(x) | -1 | 0 | 1 |
| A、{0,1} |
| B、{0,-1} |
| C、{1,-1} |
| D、{0,1,-1} |
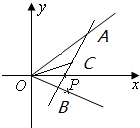 如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y= 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=AB,M、N分别是线段PB、AC上的动点,且不与端点重合,PM=AN.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=AB,M、N分别是线段PB、AC上的动点,且不与端点重合,PM=AN.