题目内容
已知x,y为正实数,且满足2x2+8y2+xy=2,则x+2y的最大值是 .
考点:基本不等式
专题:不等式的解法及应用
分析:令x+2y=t,则x=t-2y,问题等价于方程14y2-7ty+2t2-2=0有正数解,利用△≥0即可得出.
解答:
解:令x+2y=t,则x=t-2y,
方程等价为2(t-2y)2+(t-2y)y+8y2=2,
即14y2-7ty+2t2-2=0,
要使14y2-7ty+2t2-2=0有解,
则△=(-7t)2-4×14×(2t2-2)≥0,-
>0,
>0.
即63t2≤56×2,t>1.
∴t2≤
,t>1
即1<t≤
,当t=
时,y=
,x=
满足条件.
∴x+2y的最大值等于
.
故答案为:
.
方程等价为2(t-2y)2+(t-2y)y+8y2=2,
即14y2-7ty+2t2-2=0,
要使14y2-7ty+2t2-2=0有解,
则△=(-7t)2-4×14×(2t2-2)≥0,-
| -7t |
| 14 |
| 2t2-2 |
| 14 |
即63t2≤56×2,t>1.
∴t2≤
| 16 |
| 9 |
即1<t≤
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
∴x+2y的最大值等于
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题考查了通过代换转化为一元二次方程有实数根的情况,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
实数x、y满足不等式组
,且z=ax+y(a>0)取最小值的最优解有无穷多个,则实数a的取值是( )
|
A、-
| ||
| B、1 | ||
| C、2 | ||
| D、无法确定 |
过原点且倾斜角为60°的直线被圆x2+y2-4y=0所截得的弦长为( )
A、2
| ||
| B、2 | ||
C、
| ||
D、
|
 如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.
如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.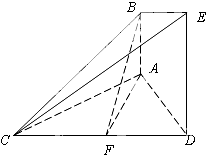 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 设地球半径为R,北纬30°圈上有A,B两地,它们的经度相差120°,则这两地间的纬度线的长为
设地球半径为R,北纬30°圈上有A,B两地,它们的经度相差120°,则这两地间的纬度线的长为