题目内容
 如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.
如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.(Ⅰ)求证:AD⊥平面B1BCC1;
(Ⅱ)求证:A1B∥平面ADC1.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)证明AD⊥平面B1BCC1,利用线面垂直的判定,证明CC1⊥AD,BC⊥AD,即可‘
(Ⅱ)连接A1C,交AC1于点O,连接OD,利用OD为△A1BC中位线,可得A1B∥OD,利用线面平行的判定,可证A1B∥平面ADC1;
(Ⅱ)连接A1C,交AC1于点O,连接OD,利用OD为△A1BC中位线,可得A1B∥OD,利用线面平行的判定,可证A1B∥平面ADC1;
解答:
(Ⅰ)证明:因为ABC-A1B1C1是正三棱柱,所以CC1⊥平面ABC
因为AD?平面ABC,所以CC1⊥AD
因为△ABC是正三角形,D为BC中点,所以BC⊥AD,
因为CC1∩BC=C,所以AD⊥平面B1BCC1.
(Ⅱ)证明:连接A1C,交AC1于点O,连接OD.
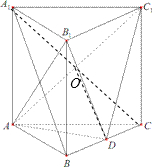
由 ABC-A1B1C1是正三棱柱,得四边形ACC1A1为矩形,O为A1C的中点.
又D为BC中点,所以OD为△A1BC中位线,
所以A1B∥OD,
因为A1B?平面ADC1,OD?平面ADC1,
所以A1B∥平面ADC1;
因为AD?平面ABC,所以CC1⊥AD
因为△ABC是正三角形,D为BC中点,所以BC⊥AD,
因为CC1∩BC=C,所以AD⊥平面B1BCC1.
(Ⅱ)证明:连接A1C,交AC1于点O,连接OD.

由 ABC-A1B1C1是正三棱柱,得四边形ACC1A1为矩形,O为A1C的中点.
又D为BC中点,所以OD为△A1BC中位线,
所以A1B∥OD,
因为A1B?平面ADC1,OD?平面ADC1,
所以A1B∥平面ADC1;
点评:本题考查线面垂直,考查线面平行,掌握线面垂直、线面平行的判定是关键.

练习册系列答案
相关题目
已知全集U=R,若集合A={x|3≤x<10},B={x|2<x≤8}.
(1)求A∩B,A∪B,(∁UA)∩(∁UB);
(2)若集合C={x|x<a},A⊆C,求a的取值范围.(结果用区间或集合表示)
(1)求A∩B,A∪B,(∁UA)∩(∁UB);
(2)若集合C={x|x<a},A⊆C,求a的取值范围.(结果用区间或集合表示)
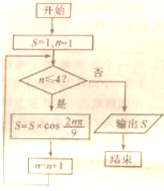
阅读如图所示的程序框图,则输出结果S的值为( )

A、-
| ||
B、-
| ||
C、
| ||
D、
|
“a>1”是“函数f(x)=x3+a在R上为单调递增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
在△ABC中,a,b,c分别为角A、B、C的对边,已知∠A=60°,b=1,面积S=
,则
等于( )
| 3 |
| a+b+c |
| sinA+sinB+sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|