题目内容
已知函数f(x)=cosx•sin(x+
)-
cos2x+
.
(1)求f(x)的最小正周期;
(2)若f(x)<m在x∈[-
,
]上恒成立,求实数m的取值范围.
| π |
| 3 |
| 3 |
| ||
| 4 |
(1)求f(x)的最小正周期;
(2)若f(x)<m在x∈[-
| π |
| 4 |
| π |
| 4 |
考点:三角函数的最值,两角和与差的正弦函数
专题:三角函数的图像与性质
分析:(1)由条件利用三角函数的恒等变换求得f(x)的解析式,再根据正弦函数的周期性求得f(x)的最小正周期.
(2)由条件利用正弦函数的定义域和值域求得f(x)的最大值,可得实数m的取值范围.
(2)由条件利用正弦函数的定义域和值域求得f(x)的最大值,可得实数m的取值范围.
解答:
解:(1)∵函数f(x)=cosx•sin(x+
)-
cos2x+
=cosx(
sinx+
cosx )-
•
+
=
sin2x-
cos2x=
sin(2x-
),
∴函数的最小正周期为 T=
=π.
(2)∵x∈[-
,
],∴2x-
∈[-
π,
π],∴f(x)max=
.
∵f(x)<m在x∈[-
,
]上恒成立,∴m>
.
| π |
| 3 |
| 3 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1+cos2x |
| 2 |
| ||
| 4 |
=
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| π |
| 3 |
∴函数的最小正周期为 T=
| 2π |
| 2 |
(2)∵x∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
| 5 |
| 6 |
| 1 |
| 6 |
| 1 |
| 4 |
∵f(x)<m在x∈[-
| π |
| 4 |
| π |
| 4 |
| 1 |
| 4 |
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,正弦函数的定义域和值域,函数的恒成立问题,属于基础题.

练习册系列答案
相关题目
下列四个命题:
①?x∈(0,+∞),(
)x<(
)x;
②?x∈(0,1),log
x>log
x;
③?x∈(0,+∞),(
)x>log
x;
④?x∈(0,
),(
)x<log
x.
其中真命题是( )
①?x∈(0,+∞),(
| 1 |
| 2 |
| 1 |
| 3 |
②?x∈(0,1),log
| 1 |
| 2 |
| 1 |
| 3 |
③?x∈(0,+∞),(
| 1 |
| 2 |
| 1 |
| 2 |
④?x∈(0,
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
其中真命题是( )
| A、①③ | B、②③ | C、②④ | D、③④ |
下列函数f(x)中,满足“对任意x1,x2∈(0,+∞),都有
<0”的是( )
| f(x1)-f(x2) |
| x1-x2 |
| A、f(x)=lnx | ||
| B、f(x)=(x-1)2 | ||
C、f(x)=
| ||
| D、f(x)=x3 |
已知全集U=R,集合M={x|x2-x>0},则∁UM=( )
| A、{x|0<x<1} |
| B、{x|0≤x≤1} |
| C、{x|x<0或x>1} |
| D、{x|x≤0或x≥1} |
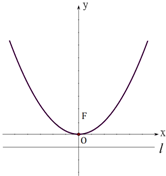 如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.
如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.