题目内容
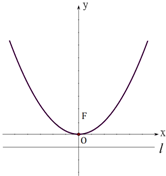 如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.
如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.(Ⅰ)求抛物线C的方程;
(Ⅱ)若点A、B在抛物线C上,且
| FB |
| OA |
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)设出抛物线C的方程,求出准线方程,利用直线与圆相切求出变量,即可得到抛物线方程;
(Ⅱ)设A(x1,y1),B(x2,y2),利用点A、B在抛物线C上,代入方程,通过
=2
,化简求解,即可得到A(
,
)点A的坐标.
(Ⅱ)设A(x1,y1),B(x2,y2),利用点A、B在抛物线C上,代入方程,通过
| FB |
| OA |
| 2 |
| 1 |
| 2 |
解答:
满分(12分).
解:(Ⅰ)依题意,可设抛物线C的方程为x2=2py(p>0),
其准线l的方程为y=-
.…(2分)
∵准线l与圆x2+y2=1相切,
∴所以圆心(0,0)到直线l的距离d=|0-(-
)|=1,解得p=2.…(4分)
故抛物线C的方程为:x2=4y. …(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),则
①…(6分)
∵F(0,1),
=(x2,y2-1),
=(x1,y1),
=2
,
∴(x2,y2-1)=2(x1,y1)=(2x1,2y1),
即
…②…(9分)
②代入①,得4
=8y1+4,
=2y1+1,
又
=4y1,所以4y1=2y1+1,解得y1=
,x1=±
,
即A(
,
)或(-
,
).…(12分)
解:(Ⅰ)依题意,可设抛物线C的方程为x2=2py(p>0),
其准线l的方程为y=-
| p |
| 2 |
∵准线l与圆x2+y2=1相切,
∴所以圆心(0,0)到直线l的距离d=|0-(-
| p |
| 2 |
故抛物线C的方程为:x2=4y. …(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),则
|
∵F(0,1),
| FB |
| OA |
| FB |
| OA |
∴(x2,y2-1)=2(x1,y1)=(2x1,2y1),
即
|
②代入①,得4
| x | 2 1 |
| x | 2 1 |
又
| x | 2 1 |
| 1 |
| 2 |
| 2 |
即A(
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
点评:本小题主要考查抛物线的标准方程、直线与圆等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想、数形结合思想等.

练习册系列答案
相关题目
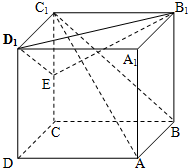 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结BC1,过点B1作BC1的垂线交CC1于E.
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结BC1,过点B1作BC1的垂线交CC1于E.