题目内容
已知抛物线y=ax2+c交x轴于A、B两点,且AB=5,交y轴于点C(0,
).
(1)求抛物线的解析式
(2)若点D为抛物线在x轴上方的任意一点,求tan∠DAB+tan∠DBA为一定值;
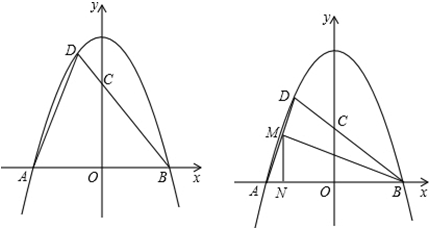
(3)若点D(-1.5,m)是抛物线y=ax2+c上一点.
①判断△ABD的形状并加以证明.
②若M是线段AD上以动点(不与A、D重合),N是线段AB上一点,设AN=t,t为何值时,线段AD上的点M总存在两个不同的位置使∠BMN=∠BDA
| 75 |
| 16 |
(1)求抛物线的解析式
(2)若点D为抛物线在x轴上方的任意一点,求tan∠DAB+tan∠DBA为一定值;
(3)若点D(-1.5,m)是抛物线y=ax2+c上一点.
①判断△ABD的形状并加以证明.
②若M是线段AD上以动点(不与A、D重合),N是线段AB上一点,设AN=t,t为何值时,线段AD上的点M总存在两个不同的位置使∠BMN=∠BDA

考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据y=ax2+c交y轴于C(0,
),可得c=
,再根据对称轴为y轴,AB=5,可得B(
,0),A(-
,0),再根据待定系数法可求抛物线的解析式;
(2)设D(x,-
x2+
),过D作DE⊥AB于E点.根据正切函数可得tan∠DAB+tan∠DBA是一个定值.
(3)①将D(-15,m)代入函数的表达式中中,可得D点坐标,再根据勾股定理得到BD=5=AB,根据等腰三角形的判断即可得到△ABD是等腰三角形.
②设AM=x,则DM=
-x,根据相似三角形的判定和性质可得关于x的方程,根据根的判别式和实际意义可得t的取值范围.
| 75 |
| 16 |
| 75 |
| 16 |
| 5 |
| 2 |
| 5 |
| 2 |
(2)设D(x,-
| 3 |
| 4 |
| 75 |
| 16 |
(3)①将D(-15,m)代入函数的表达式中中,可得D点坐标,再根据勾股定理得到BD=5=AB,根据等腰三角形的判断即可得到△ABD是等腰三角形.
②设AM=x,则DM=
| 10 |
解答:
.(1)求抛物线的解析式.(2)若点d为抛物线在x轴上方的任意一点,求证 - 初中数学 - 菁优网.mht!http://img.jyeoo.net/quiz/images/201501/183/414948fb.png) 解:(1)∵y=ax2+c交y轴于C(0,
解:(1)∵y=ax2+c交y轴于C(0,
),
∴c=
,
∵对称轴为y轴,AB=5,
∴B(
,0),A(-
,0),
将B(
,0)代入y=ax2+
,
解得a=-
.
∴y=-
x2+
;
(2)设D(x,-
x2+
),
如图,过D作DE⊥AB于E点.
∴tan∠DAB+tan∠DBA
=
+
=
+
=
,
∴tan∠DAB+tan∠DBA是一个定值.
(3)①△ABD是等腰三角形.理由如下:
将D(-1.5,m)代入y=-
x2+
中,
可得m=3,
∴D(-
,3),
∴DE=3,BE=
,
∴BD=
=5=AB,
∴△ABD是等腰三角形.
②由①可得,AD=
,
设AM=x,则DM=
-x,
∵AB=BD,
∴∠BAD=∠BDA,
∵∠BMN=∠BDA,
∴∠BMD+∠AMN=∠BMD+∠DBM,
∴∠AMN=∠DBM,
∴△AMN∽△DBM,
∵AN=t,
∴
=
,
∴
=
,
∴x2-
x-5t=0,
∵存在两个不同的位置,
∴该方程有两个不相等的实数根,
∴△=10-4×5t>0,
解得t<
.
∴当0<t<
时,总存在两个不同的位置,使∠BMN=∠BDA.
.(1)求抛物线的解析式.(2)若点d为抛物线在x轴上方的任意一点,求证 - 初中数学 - 菁优网.mht!http://img.jyeoo.net/quiz/images/201501/183/414948fb.png) 解:(1)∵y=ax2+c交y轴于C(0,
解:(1)∵y=ax2+c交y轴于C(0,| 75 |
| 16 |
∴c=
| 75 |
| 16 |
∵对称轴为y轴,AB=5,
∴B(
| 5 |
| 2 |
| 5 |
| 2 |
将B(
| 5 |
| 2 |
| 75 |
| 16 |
解得a=-
| 3 |
| 4 |
∴y=-
| 3 |
| 4 |
| 75 |
| 16 |
(2)设D(x,-
| 3 |
| 4 |
| 75 |
| 16 |
如图,过D作DE⊥AB于E点.
∴tan∠DAB+tan∠DBA
=
| DE |
| AE |
| DE |
| BE |
=
-
| ||||
t+
|
-
| ||||
|
=
| 15 |
| 4 |
∴tan∠DAB+tan∠DBA是一个定值.
(3)①△ABD是等腰三角形.理由如下:
将D(-1.5,m)代入y=-
| 3 |
| 4 |
| 75 |
| 16 |
可得m=3,
∴D(-
| 3 |
| 2 |
∴DE=3,BE=
| 5 |
| 2 |
∴BD=
| DE2+BE2 |
∴△ABD是等腰三角形.
②由①可得,AD=
| 10 |
设AM=x,则DM=
| 10 |
∵AB=BD,
∴∠BAD=∠BDA,
∵∠BMN=∠BDA,
∴∠BMD+∠AMN=∠BMD+∠DBM,
∴∠AMN=∠DBM,
∴△AMN∽△DBM,
∵AN=t,
∴
| AM |
| DB |
| AN |
| DM |
∴
| x |
| 5 |
| t | ||
|
∴x2-
| 10 |
∵存在两个不同的位置,
∴该方程有两个不相等的实数根,
∴△=10-4×5t>0,
解得t<
| 1 |
| 2 |
∴当0<t<
| 1 |
| 2 |
点评:考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的解析式,正切函数,勾股定理,等腰三角形的判定,相似三角形的判定和性质,根的判别式,综合性较强,有一定的难度.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知a>0且a≠1,下列函数中,在区间(0,a)上一定是减函数的是( )
A、f(x)=
| ||
| B、f(x)=x2-3ax+1 | ||
| C、f(x)=ax | ||
| D、f(x)=logax |
已知集合A={x|3≤x<7},B={2<x<10},则A∩B( )
| A、{x|3≤x<7} |
| B、{x|3<x<7} |
| C、{x|2≤x<7} |
| D、{x|2≤x<10} |
已知
=(x,2,0),
=(3,2-x,x),且
与
的夹角为钝角,则x的取值范围是( )
| a |
| b |
| a |
| b |
| A、x<-4 | B、-4<x<0 |
| C、0<x<4 | D、x>4 |