题目内容
已知S(t)是由函数f(x)=
-
的图象,g(x)=|x-2|-2的图象与直线x=t围成的图形的面积,则函数S(t)的导函数y=S′(t)(0<t<4)的大致图象是( )
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
A、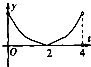 |
B、 |
C、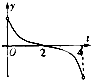 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:针对x的不同取值先去掉函数表达式中的绝对值符号,在同一坐标系中画图,结合图象处理.
解答:
解:对于函数f(x)=
-
=
,此函数中的两段都可看成反比例函数经过平移得到,
且x≥2时不难验证图象过(2,
)与(4,0);而x≤2时不难验证图象过(2,
)与(0,0);
对于函数g(x)=|x-2|-2=
,此函数中的两段都可看成直线的一部分,
x≥2时不难验证图象过(2,-2)与(4,0);而x≤2时不难验证图象过(2,-2)与(0,0);
利用上述条件在同一个平面直角坐标系内画y=f(x)与y=g(x)图象:

从图象可以看出,t从0开始增大时,直线x=t向右移动,∵S(t)是由函数f(x)=
-
的图象、g(x)=|x-2|-2的图象与直线x=t围成的图形的面积,
∴S(t)是增函数,且增的速度变化是先慢中间快再慢,
∴S′(t)的图象只有B符合.
故选:B.
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
|
且x≥2时不难验证图象过(2,
| 2 |
| 3 |
| 2 |
| 3 |
对于函数g(x)=|x-2|-2=
|
x≥2时不难验证图象过(2,-2)与(4,0);而x≤2时不难验证图象过(2,-2)与(0,0);
利用上述条件在同一个平面直角坐标系内画y=f(x)与y=g(x)图象:

从图象可以看出,t从0开始增大时,直线x=t向右移动,∵S(t)是由函数f(x)=
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
∴S(t)是增函数,且增的速度变化是先慢中间快再慢,
∴S′(t)的图象只有B符合.
故选:B.
点评:本题综合考查函数与函数图象,函数的单调性与导数的关系,属于选择题中的高档题.

练习册系列答案
相关题目
已知函数f(x)=
在[2,+∞)上单调递增,则实数a的取值范围是( )
| ||||
| a-1 |
| A、a<0或a>1 |
| B、(0,1) |
| C、a<0或1<a≤4 |
| D、0<a<1或1<a≤4 |
已知函数f(x)=lg(|x|+1),定义函数F(x)=
,若mn<0,m+n>0,则有F(m)+F(n)( )
|
| A、一定为负数 | B、等于0 |
| C、一定为正数 | D、正负不能确定 |
给出四个命题:
(1)若sin2A=sin2B,则△ABC为等腰三角形;
(2)若sinA=cosB,则△ABC为直角三角形;
(3)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.
以上正确命题的个数是( )
(1)若sin2A=sin2B,则△ABC为等腰三角形;
(2)若sinA=cosB,则△ABC为直角三角形;
(3)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.
以上正确命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
函数f(x)=
,若f(-a)+f(a)≤2f(1),则实数a取值范围是( )
|
| A、(-∞,-1]∪[1,+∞) |
| B、[-1,0] |
| C、[0,1] |
| D、[-1,1] |
在△ABC中,已知b=3,c=3
,A=30°,则角C等于( )
| 3 |
| A、30° | B、60°或120° |
| C、60° | D、120° |
己知a∈R,则“a=±1”是“a2-1+(a-1)i为纯虚数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |