题目内容
5．如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该多面体的体积为（ ）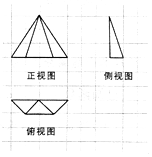
| A． | 3 | B． | 3$\sqrt{2}$ | C． | 9 | D． | 9$\sqrt{2}$ |
分析 由已知中的三视图，可得：该几何合格是一个以俯视图为底面的四棱锥，计算底面面积和高，代入椎体体积公式，可得答案．
解答 解：由已知中的三视图，可得：该几何合格是一个以俯视图为底面的四棱锥，
其底面面积S=$\frac{1}{2}$（2+4）×1=3，
高h=3，
故体积V=$\frac{1}{3}Sh$=3，
故选：A
点评 本题考查的知识点是棱锥的体积和表面积，空间几何体的三视图，难度中档．
练习册系列答案
相关题目
9．下列说法中正确的是（ ）
| A． | 经过两条平行直线，有且只有一个平面 | |
| B． | 如果两条直线平行于同一个平面，那么这两条直线平行 | |
| C． | 三点确定唯一一个平面 | |
| D． | 如果一个平面内不共线的三个点到另一平面的距离相等，则这两个平面相互平行 |
10．已知$\overrightarrow{a}$，$\overrightarrow{b}$为单位向量，且|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}-\overrightarrow{b}$|，则$\overrightarrow{a}$在$\overrightarrow{a}+\overrightarrow{b}$上的投影为（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{2\sqrt{6}}{3}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |
20．若关于x的不等式x2+ax-c＜0的解集为{x|-2＜x＜1}，且函数$y=a{x^3}+m{x^2}+x+\frac{c}{2}$在区间$（{\frac{1}{2}，1}）$上不是单调函数，则实数m的取值范围是（ ）
| A． | $（-2，-\sqrt{3}）$ | B． | $[{-3，-\sqrt{3}}]$ | C． | $（{-∞，-2}）∪（{\sqrt{3}，+∞}）$ | D． | $（{-∞，-2}）∪（{-\sqrt{3}，+∞}）$ |
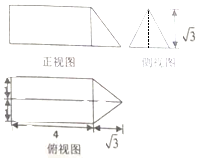
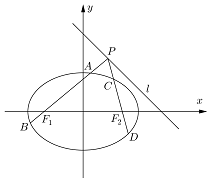已知椭圆$M：\frac{x^2}{2}+{y^2}=1$左、右焦点分别为F1、F2，点p为直线l：x+y=2上且不在x轴上的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D，O为坐标原点；