题目内容
18．（a+x）（1+x）4的展开式中x的奇数次幂项的系数之和为32，则a=（ ）| A． | -2 | B． | 2 | C． | -3 | D． | 3 |
分析 给展开式中的x分别赋值1，-1，可得两个等式，两式相减，再除以2得到答案．
解答 解：设（a+x）（1+x）4 =a0+a1x+a2x2+…+a5x5，
令x=1，则a0+a1+a2+…+a5=f（1）=16（a+1），①
令x=-1，则a0-a1+a2-…-a5=f（-1）=0．②
①-②得，2（a1+a3+a5）=16（a+1），即2×32=16（a+1），求得a=3．
故选：D．
点评 本题考查解决展开式的系数和问题时，一般先设出展开式，再用赋值法代入特殊值，相加或相减，属于基础题．
练习册系列答案
字词句段篇系列答案
相关题目
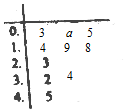已知函数f（x）=x2+$\sqrt{2}$（m-1）x+$\frac{m}{4}$，现有一组数据（该组数据数量庞大），从中随机抽取10个，绘制所得的茎叶图如图所示，且茎叶图中的数据的平均数为2．