题目内容
19.已知sinα+cosα=-$\frac{1}{2}$,则tan2α+cot2α=$\frac{46}{9}$.分析 采用两边平方,即(sinα+cosα)2=$\frac{1}{4}$,根据同角三角函数关系式和万能公式化简,得$\frac{tanα}{ta{n}^{2}α+1}$=$-\frac{3}{8}$,即tanα+$\frac{1}{tanα}$=$-\frac{8}{3}$则tan2α+cot2α=$(tanα+\frac{1}{tanα})^{2}-2$即得答案.
解答 解:由sinα+cosα=-$\frac{1}{2}$,
可得sin2α+cos2α+2sinαcosα=$\frac{1}{4}$.即sinαcosα=$\frac{sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$-\frac{3}{8}$.
同时除以cos2α,
可得:$\frac{tanα}{ta{n}^{2}α+1}$=$-\frac{3}{8}$,
得:tanα+$\frac{1}{tanα}$=$-\frac{8}{3}$
则tan2α+cot2α=$(tanα+\frac{1}{tanα})^{2}-2$=$\frac{64}{9}-2=\frac{46}{9}$.
故答案为:$\frac{46}{9}$.
点评 本题考查了同角三角函数关系式和万能公式化简能力和计算能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
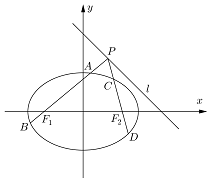 已知椭圆$M:\frac{x^2}{2}+{y^2}=1$左、右焦点分别为F1、F2,点p为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点;
已知椭圆$M:\frac{x^2}{2}+{y^2}=1$左、右焦点分别为F1、F2,点p为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点;