题目内容
 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=| 3 |
(Ⅰ)若PA=1,求证:AF⊥PC;
(Ⅱ)若二面角P-BC-A的大小为60°,则CE为何值时,三棱锥F-ACE的体积为
| 1 |
| 6 |
考点:与二面角有关的立体几何综合题,异面直线及其所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明AF⊥PC,只需证明AF⊥平面PBC;
(Ⅱ)确定∠PAB为二面角P-BC-A的一个平面角,利用三棱锥F-ACE的体积为
,求出CE.
(Ⅱ)确定∠PAB为二面角P-BC-A的一个平面角,利用三棱锥F-ACE的体积为
| 1 |
| 6 |
解答:
 (Ⅰ)证明:∵PA=AB=1,F为PB中点,
(Ⅰ)证明:∵PA=AB=1,F为PB中点,
∴AF⊥PB(1分)
又∵PA⊥平面ABCD,∴PA⊥BC(2分)
又∵ABCD是矩形,∴AB⊥BC(3分)
∴BC⊥平面PAB,而AF?平面PAB(4分)
∴AF⊥BC,∴AF⊥平面PBC(5分)
而PC?平面PBC,∴AF⊥PC(6分)
(Ⅱ)解:由(Ⅰ)知:PB⊥BC且AB⊥BC(7分)
∴∠PAB为二面角P-BC-A的一个平面角,
则∠PAB=60° (8分)
∴PA=AB×tan600=
(9分)
∴VF-ACE=
×
×EC×1×
×
=
,解得EC=
(11分)
即CE=
时,三棱锥F-ACE的体积为
(12分)
 (Ⅰ)证明:∵PA=AB=1,F为PB中点,
(Ⅰ)证明:∵PA=AB=1,F为PB中点,∴AF⊥PB(1分)
又∵PA⊥平面ABCD,∴PA⊥BC(2分)
又∵ABCD是矩形,∴AB⊥BC(3分)
∴BC⊥平面PAB,而AF?平面PAB(4分)
∴AF⊥BC,∴AF⊥平面PBC(5分)
而PC?平面PBC,∴AF⊥PC(6分)
(Ⅱ)解:由(Ⅰ)知:PB⊥BC且AB⊥BC(7分)
∴∠PAB为二面角P-BC-A的一个平面角,
则∠PAB=60° (8分)
∴PA=AB×tan600=
| 3 |
∴VF-ACE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 6 |
2
| ||
| 3 |
即CE=
2
| ||
| 3 |
| 1 |
| 6 |
点评:本题考查的知识点是空间线面垂直与线线垂直之间的转化,组合几何体的体积,熟练掌握空间线线垂直与线面垂直的之间的相互转化是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设数列{an}满足an=
(n∈N+),若数列{an}是递增数列,则b的范围是( )
|
| A、(0,3) | ||
B、(0,2+
| ||
| C、(1,3] | ||
D、(0,2+
|
设在各交通岗遇到红灯的事件是相互独立的,且概率都是0.4,则此人三次上班途中遇红灯的次数的期望为( )
| A、0.4 |
| B、1.2 |
| C、0.43 |
| D、0.6 |
函数f(x)=Msinωx(ω>0),在区间[a,b]上是增函数,且f(a)=-M,f(b)=M,则函数f(x)=Mcosωx在区间[a,b]上( )
| A、是增函数 |
| B、是减函数 |
| C、可以取得最大值M |
| D、可以取得最小值-M |
若△ABC三个内角A、B、C的对边分别为a,b,c,且a=1,∠B=45°,S△ABC=2,则sinA=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示扇形AOB,半径为2,∠AOB=
如图所示扇形AOB,半径为2,∠AOB=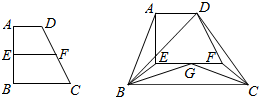 如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4.点E,F分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCD.
如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4.点E,F分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCD.