题目内容
已知cosx+3sinx=
,求tan2x.
| 5 |
考点:二倍角的正切,同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知等式左边提取
,利用两角和与差的正弦函数公式化简,表示出x,代入tanx中利用诱导公式化简,再利用两角和与差的正切函数公式整理后,将tany的值代入计算求出tanx的值,tan2x利用二倍角的正切函数公式化简后,将tanx的值代入计算即可求出值.
| 10 |
解答:
解:∵
(
cosx+
sinx)=
,即
cosx+
sinx=
,
∴sin(x+y)=
(cosy=
,siny=
,tany=3),
∴x+y=2kπ+
,k∈Z,即x=2kπ+
-y,
∴tanx=tan(2kπ+
-y)=tan(
-y)=
=
=-
,
则tan2x=
=
=-
.
| 10 |
| 1 | ||
|
| 3 | ||
|
| 5 |
| 1 | ||
|
| 3 | ||
|
| ||
| 2 |
∴sin(x+y)=
| ||
| 2 |
| 1 | ||
|
| 3 | ||
|
∴x+y=2kπ+
| π |
| 4 |
| π |
| 4 |
∴tanx=tan(2kπ+
| π |
| 4 |
| π |
| 4 |
| 1-tany |
| 1+tany |
| 1-3 |
| 1+3 |
| 1 |
| 2 |
则tan2x=
| 2tanx |
| 1-tan2x |
2×(-
| ||
1-(-
|
| 4 |
| 3 |
点评:此题考查了同角三角函数间基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
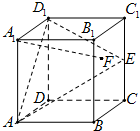 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,下列说法错误的是( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,下列说法错误的是( )| A、点F的轨迹是一条线段 |
| B、A1F与BE不在同一平面 |
| C、三棱锥F-A1D1A的体积为定值 |
| D、A1F与D1E不可能平行 |
 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=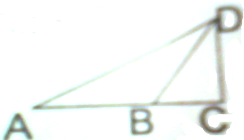 如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100
如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100