题目内容
函数f(x)=Msinωx(ω>0),在区间[a,b]上是增函数,且f(a)=-M,f(b)=M,则函数f(x)=Mcosωx在区间[a,b]上( )
| A、是增函数 |
| B、是减函数 |
| C、可以取得最大值M |
| D、可以取得最小值-M |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由函数f(x)=Msinωx(ω>0)在区间[a,b]上是增函数,且f(a)=-M,f(b)=M,可利用赋值法进行求解即可.
解答:
解:∵函数f(x)在区间[a,b]上是增函数,且f(a)=-M,f(b)=M
采用特殊值法:令ω=1,则f(x)=Msinx,
设区间为[-
,
],
∵M>0,g(x)=Mcosx在[-
,
]上不具备单调性,但有最大值M,
故选:C.
采用特殊值法:令ω=1,则f(x)=Msinx,
设区间为[-
| π |
| 2 |
| π |
| 2 |
∵M>0,g(x)=Mcosx在[-
| π |
| 2 |
| π |
| 2 |
故选:C.
点评:本题综合考查了正弦函数与余弦函数的图象及性质,利用整体思想进行求值,在解题时要注意特殊值的应用.

练习册系列答案
相关题目
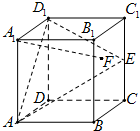 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,下列说法错误的是( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,下列说法错误的是( )| A、点F的轨迹是一条线段 |
| B、A1F与BE不在同一平面 |
| C、三棱锥F-A1D1A的体积为定值 |
| D、A1F与D1E不可能平行 |
已知等差数列{an}的前13项和S13=39,则a2+a4+a15=( )
| A、3 | B、6 | C、9 | D、12 |
已知c>0且c≠1,设命题p:函数f(x)=logcx为减函数,命题q:函数g(x)=x+
>
(x∈[
,2])恒成立,若p且q为假命题,p或q为真命题,则实数c的取值范围为( )
| 1 |
| x |
| 1 |
| c |
| 1 |
| 2 |
A、(0,
| ||
| B、(1,+∞) | ||
C、(0,
| ||
D、(0,
|
从6名志愿者(其中4名男生,2名女生)中选出4名义务参加某项宣传活动,要求男女生都有,则不同的选法种数是( )
| A、12种 | B、14种 |
| C、36种 | D、72种 |

 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=