题目内容
设数列{an}满足an=
(n∈N+),若数列{an}是递增数列,则b的范围是( )
|
| A、(0,3) | ||
B、(0,2+
| ||
| C、(1,3] | ||
D、(0,2+
|
考点:数列的函数特性
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:根据数列的递增性,转化为函数的单调性即可得到结论.
解答:
解:∵数列{an}是递增数列,
∴数列{an},满足,
则
,
即
,
则
,
解得0<b<3,
即实数a的取值范围是(0,3),
故选:A.
∴数列{an},满足,
则
|
即
|
则
|
解得0<b<3,
即实数a的取值范围是(0,3),
故选:A.
点评:本题主要考查数列的单调性,利用函数的单调性是解决本题的关键,注意分段函数的单调性之间的关系.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
已知全集U=R,集合A={x|lgx≤0},B={x|2x≤1},则A∪B=( )
| A、(-∞,0] |
| B、(-∞,1] |
| C、[0,+∞) |
| D、[1,+∞) |
等比数列{an}的各项均为正数,若a2•a9=9,则log3a1+log3a2+…+log3a10=( )
| A、12 |
| B、10 |
| C、8 |
| D、2+log35 |
“x>1”是“x2-x>0”的( )
| A、充分而不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
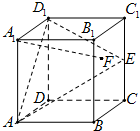 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,下列说法错误的是( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,下列说法错误的是( )| A、点F的轨迹是一条线段 |
| B、A1F与BE不在同一平面 |
| C、三棱锥F-A1D1A的体积为定值 |
| D、A1F与D1E不可能平行 |

 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=