题目内容
设在各交通岗遇到红灯的事件是相互独立的，且概率都是0.4，则此人三次上班途中遇红灯的次数的期望为（ ）
| A、0.4 |
| B、1.2 |
| C、0.43 |
| D、0.6 |
考点：二项分布与n次独立重复试验的模型,离散型随机变量的期望与方差
专题：计算题,概率与统计
分析：依题意，此人上班途中遇红灯的次数为X，则X～B（3，0.4），利用公式可得结论．
解答：
解：设此人上班途中遇红灯的次数为X，则X～B（3，0.4）
∴E（X）=3×0.4=1.2
故选B．
∴E（X）=3×0.4=1.2
故选B．
点评：本题考查二项分布，考查数学期望，考查学生利用数学知识解决实际问题，属于基础题．
练习册系列答案
相关题目
“x＞1”是“x2-x＞0”的（ ）
| A、充分而不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
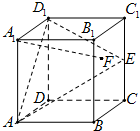在棱长为1的正方体ABCD-A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内（包括边）的动点，且A1F∥平面D1AE，下列说法错误的是（ ）| A、点F的轨迹是一条线段 |
| B、A1F与BE不在同一平面 |
| C、三棱锥F-A1D1A的体积为定值 |
| D、A1F与D1E不可能平行 |
设点O是面积为4的△ABC内部一点，且有
+
+2
=
，则△AOC的面积为（ ）
| OA |
| OB |
| OC |
| 0 |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
已知等差数列{an}的前13项和S13=39，则a2+a4+a15=（ ）
| A、3 | B、6 | C、9 | D、12 |
已知c＞0且c≠1，设命题p：函数f（x）=logcx为减函数，命题q：函数g（x）=x+
＞
（x∈[
，2]）恒成立，若p且q为假命题，p或q为真命题，则实数c的取值范围为（ ）
| 1 |
| x |
| 1 |
| c |
| 1 |
| 2 |
A、（0，
| ||
| B、（1，+∞） | ||
C、（0，
| ||
D、（0，
|
如图所示，PA⊥平面ABCD，ABCD是矩形，AB=1，AD=