题目内容
3.已知F为双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的左焦点,A(1,4),P是C右支上一点,当△APF周长最小时,点F到直线AP的距离为$\frac{32}{5}$.分析 设双曲线的右焦点为F′(4,0),由题意,A,P,F′共线时,△APF周长最小,求出直线AP的方程,即可求出点F到直线AP的距离.
解答 解:设双曲线的右焦点为F′(4,0),由题意,A,P,F′共线时,△APF周长最小,直线AP的方程为y=$\frac{4}{1-4}$(x-4),即4x+3y-16=0,
∴点F到直线AP的距离为$\frac{|-16-16|}{\sqrt{16+9}}$=$\frac{32}{5}$,
故答案为:$\frac{32}{5}$
点评 本题考查双曲线的方程与性质,考查点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
13.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦点的渐近线的距离为2,且双曲线的一条渐近线与直线x-2y+3=0平行,则双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ |
11.a>b的一个充分不必要条件是( )
| A. | a=1,b=0 | B. | $\frac{1}{a}$<$\frac{1}{b}$ | C. | a2>b2 | D. | a3>b3 |
18.在△ABC中,若BC=2,A=120°,则$\overrightarrow{AB}$•$\overrightarrow{CA}$的最大值为( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
15.圆x2+y2-6x-2y+3=0的圆心到直线x+ay-1=0的距离为1,则a=( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
13.函数$y=\frac{6}{{{2^x}+{3^x}}}(-1≤x≤1)$的最小值为( )
| A. | 3 | B. | $\frac{6}{5}$ | C. | $\frac{36}{5}$ | D. | $\frac{6}{13}$ |
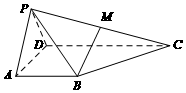 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,$AB=AD=\frac{1}{2}CD$,AB⊥AD,AB∥CD,点M是PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,$AB=AD=\frac{1}{2}CD$,AB⊥AD,AB∥CD,点M是PC的中点.