函数$y=\frac{6}{{{2^x}+{3^x}}}$的最小值为( )A．3B．$\frac{6}{5}$C．$\frac{36}{5}$D．$\frac{6}{13}$ 题目和参考答案——青夏教育精英家教网—

题目内容

13．函数$y=\frac{6}{{{2^x}+{3^x}}}（-1≤x≤1）$的最小值为（　　）

A．

B．

$\frac{6}{5}$

C．

$\frac{36}{5}$

D．

$\frac{6}{13}$

分析利用指数函数与反比例函数的单调性即可得出．

解答解：由于函数y=2^x+3^x在x∈[-1，1]上单调递增，∴$y=\frac{6}{{2}^{x}+{3}^{x}}$在x∈[-1，1]上单调递减，
∴函数f（x）=$y=\frac{6}{{{2^x}+{3^x}}}（-1≤x≤1）$的最小值为f（1）=$\frac{6}{5}$．
故选：B．

点评本题考查了指数函数与反比例函数的单调性，考查了推理能力与计算能力，属于基础题．

练习册系列答案

4．${（{x^2}-\frac{1}{2x}）^6}$展开式中的常数项是$\frac{15}{16}$．

1．以下说法正确的是（　　）
①若x，y∈R，则“x=y“是“$xy≥{（\frac{x+y}{2}）^2}$“的充要条件．
②命题“已知x，y∈R，若x+y≠3，则x≠2或y≠1”是真命题
③“x²+2x≥ax在x∈[1，2]恒成立”?“对于x∈[1，2]，有（x²+2x）_min≥（ax）_max”
④命题“若a=-1，则函数f（x）=ax²+2x-1只有一个零点”的逆命题为真命题．

8．

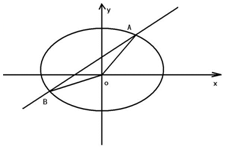已知椭圆C的中心在坐标原点，一个焦点的坐标为$（\sqrt{3}，0）$，椭圆C经过点P$（1，\frac{{\sqrt{3}}}{2}）$．
（1）求椭圆C的方程；
（2）设直线y=kx+b与椭圆C交于A，B两点，若|AB|=2，△AOB的面积S=1，求直线AB的方程．

18．已知全集U=R，集合A={x|x＜a或x＞2-a，（a＜1）}，集合B={x|$tan（πx-\frac{π}{3}）=-\sqrt{3}\}$．
（Ⅰ）求集合∁_UA与B；
（Ⅱ）当-1＜a≤0时，集合C=（∁_UA）∩B恰好有3个元素，求集合C．

5．正项等比数列{a_n}的前n项和为S_n，若${a_1}=1，\;{S_3}=\frac{7}{4}$，则a₆=$\frac{1}{32}$．

2．已知直角坐标平面O-XY上的动点P到定点F（1，0）的距离比它到y轴的距离多1，记P点的轨迹为曲线C，则直线l：2x-3y+4=0与曲线C的交点的个数为（　　）

13．

如图所示，已知G，G₁分别是棱长为4的正方体ABCD-A₁B₁C₁D₁的下底面和上地面的中心，点P在线段GG₁上运动，点Q在下底面ABCD内运动，且始终保持PQ=2，则线段PQ的中点M运动形成的曲面与正方体下底面所围成的几何体的体积为$\frac{2π}{3}$．

试题分类