题目内容
18.在△ABC中,若BC=2,A=120°,则$\overrightarrow{AB}$•$\overrightarrow{CA}$的最大值为( )| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
分析 由$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,⇒4=AC2+AB2-2AC•ABcosA⇒4=AC2+AB2+AC•AB≥2A•CAB+AC•AB=3AC•AB⇒AC•AB,$\overrightarrow{AB}$•$\overrightarrow{CA}$=AC•ABcos120°即可
解答 解:∵$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,∴$(\overrightarrow{BC})^{2}=(\overrightarrow{AC}-\overrightarrow{AB})^{2}$⇒4=AC2+AB2-2AC•ABcosA⇒4=AC2+AB2+AC•AB≥2A•CAB+AC•AB=3AC•AB⇒AC•AB≤$\frac{4}{3}$
∴$\overrightarrow{AB}$•$\overrightarrow{CA}$=AC•ABcos120°≤$\frac{2}{3}$,则$\overrightarrow{AB}$•$\overrightarrow{CA}$的最大值为 $\frac{2}{3}$,
故选:A.
点评 考查向量减法的几何意义,数量积的运算及其计算公式,涉及了不等式a2+b2≥2ab的应用,属于基础题.

练习册系列答案
相关题目
6.设实数x,y满足约束条件$\left\{\begin{array}{l}x-2y-5≤0\\ x+y-4≤0\\ 3x+y-10≥0\end{array}\right.$,则z=x2+y2的最小值为( )
| A. | $\sqrt{10}$ | B. | 10 | C. | 8 | D. | 5 |
13.等比数列{an}中,a2+a4=20,a3+a5=40,则a6=( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
10.若l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
| A. | 若l∥α,m∥α,则l∥m | B. | 若l⊥m,m?α,则l⊥α | C. | 若l∥α,m?α,则l∥m | D. | 若l⊥α,l∥m,则m⊥α |
7.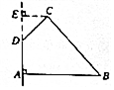 如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,则四边形ABCD绕AD旋转一周所成几何体的表面积为( )
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,则四边形ABCD绕AD旋转一周所成几何体的表面积为( )
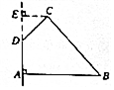 如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,则四边形ABCD绕AD旋转一周所成几何体的表面积为( )
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,则四边形ABCD绕AD旋转一周所成几何体的表面积为( )| A. | (60+4$\sqrt{2}$)π | B. | (60+8$\sqrt{2}$)π | C. | (56+8$\sqrt{2}$)π | D. | (56+4$\sqrt{2}$)π |
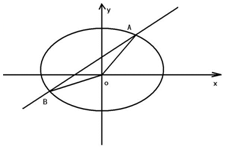 已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.
已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.