题目内容
8.椭圆x2+9y2=9的长轴长为6.分析 将椭圆化为标准方程,求得a=3,即可得到长轴长2a.
解答 解:椭圆x2+9y2=9即为$\frac{{x}^{2}}{9}$+y2=1,
即有a=3,b=1,
则长轴长为2a=6.
故答案为:6.
点评 本题考查椭圆的方程和性质,注意将椭圆方程化为标准方程,考查运算能力,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
4.在等差数列{an}中,前n项和为Sn,且S2013=-2013,a1008=3,则S2014等于( )
| A. | 2014 | B. | -2014 | C. | 1007 | D. | -1007 |
13.若椭圆和双曲线C:2x2-2y2=1有相同的焦点,且该椭圆经过点$({1,-\frac{3}{2}})$,则椭圆的方程为( )
| A. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{5}=1$ | D. | $\frac{x^2}{9}+\frac{y^2}{5}=1$ |
17.某几何体的三视图如图所示,该几何体的侧面积( )
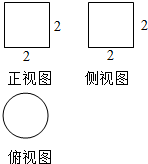

| A. | 5π | B. | 4π | C. | 3π | D. | 2π |
18.已知点A(1,2,-1),点C与点A关于平面xOy对称,点B与点A关于x轴对称,则线段BC的长为( )
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{7}$ |
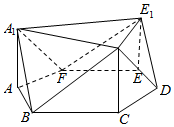 已知如图几何体A1C1E1-ABCDEF底面是边长为2的六变形,AA1,CC1,EE1长度为2且都垂直与底面,
已知如图几何体A1C1E1-ABCDEF底面是边长为2的六变形,AA1,CC1,EE1长度为2且都垂直与底面,