题目内容
13.若椭圆和双曲线C:2x2-2y2=1有相同的焦点,且该椭圆经过点$({1,-\frac{3}{2}})$,则椭圆的方程为( )| A. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{5}=1$ | D. | $\frac{x^2}{9}+\frac{y^2}{5}=1$ |
分析 求得双曲线的焦点坐标,可得椭圆的c=1,再由椭圆的定义,运用两点的距离公式计算可得a=2,由a,b,c的关系,可得b,进而得到椭圆方程.
解答 解:双曲线C:2x2-2y2=1的焦点为(-1,0),(1,0),
即有椭圆的c=1,
由椭圆的定义可得2a=$\sqrt{(1+1)^{2}+\frac{9}{4}}$+$\sqrt{0+\frac{9}{4}}$=4,
解得a=2,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
故选:B.
点评 本题考查椭圆的方程的求法,注意运用双曲线的焦点,以及椭圆的定义,考查运算能力,属于基础题.

练习册系列答案
相关题目
1.已知球O的直径PQ=4,A、B、C是球O球面上的三点,△ABC是等腰直角三角形,且∠ACB=90°,∠APQ=∠BPQ=∠CPQ=30°,则三棱锥P-ABC的体积为( )
| A. | $\frac{3\sqrt{3}}{4}$ | B. | 3 | C. | $\frac{3\sqrt{3}}{2}$ | D. | 6 |
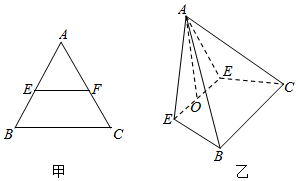 如图甲,在边长为4的等边△ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将△AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.
如图甲,在边长为4的等边△ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将△AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.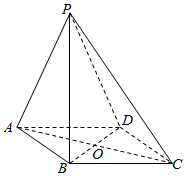 如图,四棱锥P-ABCD底面ABCD为平行四边形,且AC∩BD=O,PA=PC,PB⊥BD,平面PBD⊥平面PAC.
如图,四棱锥P-ABCD底面ABCD为平行四边形,且AC∩BD=O,PA=PC,PB⊥BD,平面PBD⊥平面PAC.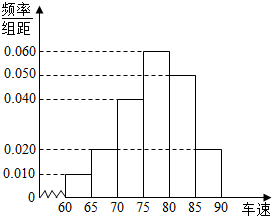 2014年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图的频率分布直方图.
2014年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图的频率分布直方图.