题目内容
1.已知数列{an}满足an+1=1-$\frac{1}{a_n}$,a1=2,记数列{an}的前n项之积为Tn,则T2015=-1.分析 由已知an+1=1-$\frac{1}{a_n}$,a1=2,可求数列的前几项,进而可得数列的周期性规律,代入即可求得答案.
解答 解:由a1=2,an+1=1-$\frac{1}{{a}_{n}}$,
得a2=1-$\frac{1}{{a}_{1}}$=$\frac{1}{2}$,a3=1-$\frac{1}{{a}_{2}}$=-1,a4=1-$\frac{1}{{a}_{3}}$=2,…,
由上可知,数列的项重复出现,呈现周期性,周期为3.
且T3=a1a2a3=-1,2015=3×671+2,
∴T2015=(-1)671•a1a2=-1.
故答案为:-1.
点评 本题考查数列的递推公式,数列的函数性质--周期性.发现周期性并利用是本题的关键,是中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
11.已知tan2θ=$\frac{3}{4}$,θ∈(0,$\frac{π}{4}$),则$\frac{si{n}^{2}θ+cos2θ}{sin(θ+\frac{π}{4})}$的值为( )
| A. | $\frac{9\sqrt{5}}{20}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{\sqrt{10}}{10}$ |
1.已知球O的直径PQ=4,A、B、C是球O球面上的三点,△ABC是等腰直角三角形,且∠ACB=90°,∠APQ=∠BPQ=∠CPQ=30°,则三棱锥P-ABC的体积为( )
| A. | $\frac{3\sqrt{3}}{4}$ | B. | 3 | C. | $\frac{3\sqrt{3}}{2}$ | D. | 6 |
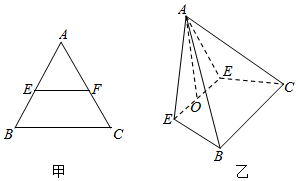 如图甲,在边长为4的等边△ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将△AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.
如图甲,在边长为4的等边△ABC中,点E,F分别为AB,AC上一点,且EF∥BC,EF=2a,沿EF将△AEF折起,使得平面AEF⊥平面EFCB,形成一个如图乙所示的四棱锥,设O为EF的中点.