题目内容
2.设抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4的点,|AF|=5.(1)求抛物线C的方程;
(2)设过点F且斜率为1的直线l交抛物线C于M,N两点,O为坐标原点,求△OMN的面积.
分析 (1)利用抛物线的定义求出抛物线的p,即可顶点抛物线方程.
(2)求出抛物线的焦点坐标F(1,0),直线AB的方程为y=x-1,联立$\left\{{\begin{array}{l}{y=x-1}\\{{y^2}=4x}\end{array}}\right.$消y得:x2-6x+1=0,利用韦达定理求出|AB|,求出O到直线AB的距离,然后求解数据线的面积.
解答 解:(1)抛物线C的准线方程为:$x=-\frac{p}{2}$
由抛物线的定义可知:$\frac{p}{2}=5-4$
∴p=2
∴抛物线C的标准方程为y2=4x. …(4分)
(2)由已知,F(1,0),直线AB的方程为y=x-1,…(6分)
联立$\left\{{\begin{array}{l}{y=x-1}\\{{y^2}=4x}\end{array}}\right.$消y得:x2-6x+1=0,
所以x1+x2=6,…(8分)…(8分)
所以|AB|=x1+x2+p=8,…(10分)
又因为O到直线AB的距离$d=\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$,
所以${S_{△OMN}}=\frac{1}{2}×\frac{{\sqrt{2}}}{2}×8=2\sqrt{2}$. …(12分)
点评 本题考查抛物线的简单性质的应用,直线与抛物线的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
13.已知集合A={1,2,3},B={y|y=x-2,x∈A},则A∩B=( )
| A. | {1} | B. | {4} | C. | {1,3} | D. | {1,4} |
10.以A(1,3)和B(-5,1)为端点的线段AB的中垂线方程是( )
| A. | 3x-y+8=0 | B. | x-3y+8=0 | C. | 3x+y+8=0 | D. | 3x+y+4=0 |
14.已知函数f(x)=ax3+bx2+cx+d的图象如图所示,则下列结论正确的是( )


| A. | a>0,c<0,d>0 | B. | a>0,c>0,d<0 | C. | a<0,c<0,d<0 | D. | a<0,c>0,d<0 |
11.已知非零常数α是函数y=x+tanx的一个零点,则(α2+1)(1+cos2α)的值为( )
| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | $2-\sqrt{2}$ |
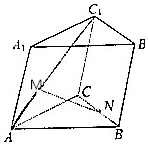 如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).
如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).
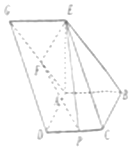 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.