题目内容
17.已知某几何体的三视图如图所示,则该几何体的体积为54π.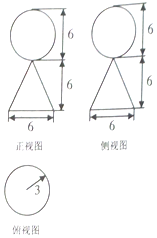
分析 由三视图还原原几何体,可得原几何体是下面为圆锥,上面为球的组合体.再由圆锥的体积公式及球的体积公式求得答案.
解答 解:由三视图可知,原几何体是下面为圆锥,上面为球的组合体.
则其体积为V=$\frac{1}{3}×π×{3}^{2}×6+\frac{4}{3}×π×{3}^{3}=54π$.
故答案为:54π.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状,是基础题.

练习册系列答案
相关题目
7.设函数f(x)=$\left\{\begin{array}{l}{2sinx,0≤x≤π}\\{{x}^{2},x<0}\end{array}\right.$,则函数y=f(f(x))-1的零点的个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 无数个 |
8.将圆周20等份,按照逆时针方向依次编号为1、2、…20,若从某一点开始,沿圆周逆时针方向行走,点的编号是数字几,就走几段弧长,称这种走法为一次“移位”,如:小明在编号为1的点,他应走1段弧长,即从1→2为第一次“移位”,这时他到达编号为2的点,然后从2→3→4为第二次“移位”,若某人从编号为3的点开始,沿逆时针方向,按上述“移位”方法行走,“移位”a次刚好到达编号为16的点,又满足|a-2016|的值最小,则a的值为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
12.已知向量$\overrightarrow a=({1-t\;\;,\;\;2t-1\;\;,\;\;0})$,$\overrightarrow b=({2\;\;,\;\;t\;\;,\;\;t})$(t∈R),则$|{\overrightarrow b-\overrightarrow a}|$的最小值是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
6.集合A={x|x≤a},B={1,2},A∩B=∅,则a的取值范围为( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (2,+∞) | D. | (-∞,2) |
7.已知a>0且a≠1,如图所示的程序框图的输出值y∈[4,+∞),则实数a的取值范围是( )
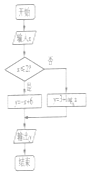

| A. | (1,2] | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | [2,+∞) |
 如图,四棱锥P-ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{13}$,M,N分别为BC,PA的中点
如图,四棱锥P-ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{13}$,M,N分别为BC,PA的中点