题目内容

5．如图，在平行四边形ABCD中，∠ABD=90°，2AB2+BD2=4，若将其沿BD折成直二面角A-BD-C，则三棱锥A-BCD的外接球的表面积为（　　）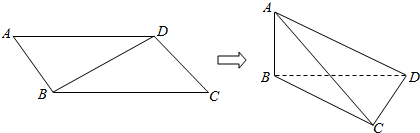
A．4πB．8πC．12πD．16π

分析 确定三棱锥A-BCD的外接球的直径，根据2AB2+BD2-4=0，确定三棱锥A-BDC的外接球的半径，即可求得棱锥A-BDC的外接球的表面积．

解答 解：∵平行四边形ABCD中，AB⊥BD，沿BD折成直二面角A-BD-C，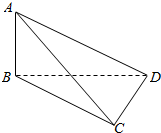

∴三棱锥A-BCD的外接球的直径为AC，且AC2=AB2+BD2+CD2=2AB2+BD2=4，
∴三棱锥A-BDC的外接球的半径为1，
∴三棱锥A-BDC的外接球的表面积是4π
故选：A．

点评 本题考查球的表面积，考查学生的计算能力，解题的关键是确定三棱锥A-BCD的外接球的直径，属于中档题．

练习册系列答案
相关题目
14．已知两点O（0，0），A（6，0），圆C以线段OA为直径．
（1）求圆C的方程；
（2）若直线1：x-y-1=0与圆C相交于M，N两点，求弦MN的长．
16．在△ABC中，三个内角A、B、C所对的边分别为a、b、c，若内角A、B、C依次成等差数列，且不等式-x2+6x-8＞0的解集为{x|a＜x＜c}，则S△ABC等于（　　）
A．$\sqrt{3}$B．2$\sqrt{3}$C．3$\sqrt{3}$D．4$\sqrt{3}$
13．设集合M={a1，a2，…an}（n∈N+），对M的任意非空子集A，定义f（A）为A中的最大元素，当A取遍M的所有非空子集时，对应的f（A）的和为Tn，若an=2n-1则：①T3=21，②Tn=$\frac{{4}^{n}-1}{3}$．
20．已知函数$f（x）=\sqrt{3}sin2x+2sin（x-\frac{π}{4}）sin（x+\frac{π}{4}）$．
（Ⅰ）求函数f（x）图象的对称轴方程；
（Ⅱ）求函数f（x）在区间$[-\frac{π}{12}，\frac{π}{2}]$上的值域．
10．如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图，则这个平面图形的面积是（　　）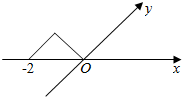 
A．$2\sqrt{2}$B．$\sqrt{2}$C．1D．$\frac{{\sqrt{2}}}{2}$
17．将单位圆经过伸缩变换：φ：$\left\{\begin{array}{l}{x′=λx}\\{y′=μy}\end{array}\right.$（λ＞0，μ＞0）得到曲线C：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1
（1）求实数λ，μ的值；
（2）以原点O 为极点，x 轴为极轴建立极坐标系，将曲线C 上任意一点到极点的距离ρ（ρ≥0）?表示为对应极角θ（0≤θ＜2π）的函数，并探求θ为何值时，ρ取得最小值？
14．设定义在R上的函数f（x）满足以下条件：
（1）f（x）+f（-x）=0；
（2）f（x+1）=f（x-1）；   
（3）当0≤x≤1时，f（x）=2x-1，
则$f（\frac{1}{2}）+f（\frac{3}{2}）+f（1）+f（2）+f（4）+f（\frac{9}{2}）$=$\sqrt{2}$．
15．设函数f（x）（x∈R）满足f（x+π）=f（x）+sinx，当0≤x≤π时，f（x）=0．则f（$\frac{23π}{6}$）=$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网