题目内容
在锐角△ABC中,a,b,c分别是内角A,B,C所对的边,已知2asinC=
c.
(Ⅰ)求角A的大小;
(Ⅱ)若b+c=4,△ABC的面积等于
,求a,b,c.
| 3 |
(Ⅰ)求角A的大小;
(Ⅱ)若b+c=4,△ABC的面积等于
| 3 |
考点:正弦定理,余弦定理
专题:计算题,解三角形
分析:(Ⅰ)利用正弦定理把已知等式的边转化成角的正弦,求得sinA的值,进而求得A.
(Ⅱ)利用面积公式求得bc的值,进而根据b+c联立方程可求得b,c,最后根据余弦定理求得a.
(Ⅱ)利用面积公式求得bc的值,进而根据b+c联立方程可求得b,c,最后根据余弦定理求得a.
解答:
解:(Ⅰ)∵在锐角△ABC中,2asinC=
c,
∴由正弦定理得:2sinAsinC=
sinC,又sinC>0,
∴sinA=
,
∵A为锐角,
∴A=
.
(Ⅱ)∵S△ABC=
bcsinA=
,
∴bc=4.
∴
,
∴b=2,c=2.
∵a2=b2+c2-bc=4,
∴a=2.
| 3 |
∴由正弦定理得:2sinAsinC=
| 3 |
∴sinA=
| ||
| 2 |
∵A为锐角,
∴A=
| π |
| 3 |
(Ⅱ)∵S△ABC=
| 1 |
| 2 |
| 3 |
∴bc=4.
∴
|
∴b=2,c=2.
∵a2=b2+c2-bc=4,
∴a=2.
点评:本题主要考查应用正、余弦定理,三角形面积公式等知识解三角形;考查运算求解的能力、化归与转化、解方程的思想.

练习册系列答案
相关题目
已知命题p:?x∈(-∞,0),2x<3x,命题q:?x∈(0,1),log2x<0,则下列命题为真命题的是( )
| A、p∧q |
| B、p∨(﹁q) |
| C、(﹁p)∧q |
| D、p∧(﹁q) |
复数z=3-4i,则|z|=( )
| A、3 | B、4 | C、1 | D、5 |
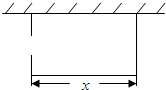 某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.