题目内容
已知函数f（x）=3sinx+4cosx，则函数f（x）的最大值为 ．
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：由辅助角公式可得f（x）=5sin（x+θ），再根据正弦函数的值域可得f（x）的最大值．
解答：
解：函数f（x）=3sinx+4cosx 5（
sinx+
cosx），
令cosθ=
，sinθ=
，θ∈[0，2π）．
则由辅助角公式可得f（x）=5sin（x+θ），根据正弦函数的值域可得f（x）的最大值为5，
故答案为：5．
| 3 |
| 5 |
| 4 |
| 5 |
令cosθ=
| 3 |
| 5 |
| 4 |
| 5 |
则由辅助角公式可得f（x）=5sin（x+θ），根据正弦函数的值域可得f（x）的最大值为5，
故答案为：5．
点评：本题主要考查辅助角公式，正弦函数的值域，属于中档题．
练习册系列答案
相关题目
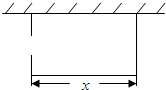某校要建一个面积为450平方米的矩形球场，要求球场的一面利用旧墙，其他各面用钢筋网围成，且在矩形一边的钢筋网的正中间要留一个3米的进出口（如图）．设矩形的长为x米，钢筋网的总长度为y米．