题目内容

已知点M与x轴的距离和点M与点F（0，4）的距离相等，求点M的轨迹方程．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用直接法，设出动点为P的坐标（x，y），利用条件建立方程并化简即可．
解答： 解：由题意设动点M（x，y），则
∵点M与x轴的距离和点M与点F（0，4）的距离相等，
∴|y|=
x2+(y-4)2
，
∴y=
1
8
x2+2，
即点M的轨迹方程是y=
1
8
x2+2．
点评：直接法求动点的轨迹方程是求动点的轨迹方程的基本方法．
练习册系列答案
相关题目
已知函数f（x）=4cosωx•sin（ωx-
π
6
）+1（ω＞0）的最小正周期是π．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）求f（x）在[
π
8
，
3π
8
]上的最大值和最小值．
从一个底面半径和高都是R的圆柱中，挖去一个以圆柱的上底为底，下底面的中心为顶点的圆锥，如果用一个与圆柱下表面距离等于L，并且平行于底面的平面去截此几何体，求所截得的面积．
已知函数f（x）=2sin（ωx），其中常数ω＞0．
（1）当ω=2时，x∈[-
π
6
，
π
3
]，求f（x）的值域；
（2）若y=f（x）在[-
π
4
，
2π
3
]单调递增，求ω的取值范围．
我国是水资源较贫乏的国家之一，各地采用价格调控等手段来达到节约用水的目的，某市每户每月用水收费办法是：水费=基本费+超额费+定额损耗费．且有如下两条规定：
①若每月用水量不超过最低限量m立方米，只付基本费10元加上定额损耗费2元；
②若用水量超过m立方米时，除了付以上同样的基本费和定额损耗费外，超过部分每立方米加付n元的超额费．
解答以下问题：
（1）写出每月水费y（元）与用水量x（立方米）的函数关系式；
（2）若该市某家庭今年一季度每月的用水量和支付的费用如下表所示：
月份 用水量（立方米） 水费（元）
一 5 17
二 6 22
三 3.5 12
试判断该家庭今年一、二、三各月份的用水量是否超过最低限量，并求m，n的值．
数列{an}的前n项为Sn，Sn=2an-3n（n∈N*）．
（1）证明：数列{an+3}是等比数列；
（2）求数列{an}的通项公式an．
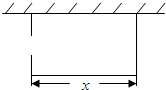某校要建一个面积为450平方米的矩形球场，要求球场的一面利用旧墙，其他各面用钢筋网围成，且在矩形一边的钢筋网的正中间要留一个3米的进出口（如图）．设矩形的长为x米，钢筋网的总长度为y米．
（Ⅰ）列出y与x的函数关系式，并写出其定义域；
（Ⅱ）问矩形的长与宽各为多少米时，所用的钢筋网的总长度最小？
（Ⅲ）若由于地形限制，该球场的长和宽都不能超过25米，问矩形的长与宽各为多少米时，所用的钢筋网的总长度最小？
定义在（-1，1）上的函数f（x）是减函数，且满足f（1-a）＜f（a），求实数a取值范围．
命题：“能被2或5整除的数，末位数字是0”的逆否命题是：
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网