题目内容
设平面内的向量
=（1，7），
=（5，1），
=（2，1），P是直线OM上的一个动点，且
•
=-8．求：
（Ⅰ）向量
的坐标；
（Ⅱ）向量
与
夹角的余弦值．
| OA |
| OB |
| OM |
| PA |
| PB |
（Ⅰ）向量
| OP |
（Ⅱ）向量
| PA |
| PB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意，可设
=（x，y），再由点P在直线OM上，得到
，
共线，由此共线条件得到x，y之间的关系，代入
•
=-8，解出x，y的值，即可求出
的坐标及
，
的坐标，再由夹角的向量表示公式求出∠APB的余弦值．
| OP |
| OP |
| OM |
| PA |
| PB |
| OP |
| PA |
| PB |
解答：
解：（Ⅰ）由题意，可设
=（x，y），再由点P在直线OM上，
∴
，
共线，
=（2，1），
∴x-2y=0，即x=2y，
=（2y，y），
（Ⅱ）∵
=
-
=（1-2y，7-y），
=
-
=（5-2y，1-y），
∴
•
=（1-2y）（5-2y）+（7-y）（1-y）=5y2-20y+12=-8，
解得y=2，x=4，
此时
=（4，2），
=（-3，5），
=（1，-1），
∴cos∠APB=
=
=-
．
| OP |
∴
| OP |
| OM |
| OM |
∴x-2y=0，即x=2y，
| OP |
（Ⅱ）∵
| PA |
| OA |
| OP |
| PB |
| OB |
| OP |
∴
| PA |
| PB |
解得y=2，x=4，
此时
| OP |
| PA |
| PB |
∴cos∠APB=
| ||||
|
|
| -8 | ||||
|
4
| ||
|
点评：本题考查了向量共线的条件、向量的坐标运算、数量积的坐标表示、向量的模的求法及利用数量积求两个向量夹角的余弦．
练习册系列答案
相关题目
要得到函数y=sinx的图象，只需将函数y=cos（x-
）+2的图象沿向量
平移得到，则
为（ ）
| π |
| 3 |
| a |
| a |
A、（-
| ||
B、（
| ||
C、（-
| ||
D、（
|
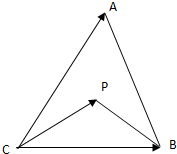如图示，已知A、B、C为平面上的三个定点，∠ACB=60°，动点P在∠ACB的平分线上，记