题目内容
若曲线y=kx2的一条切线与直线y=-4x+3垂直且切点纵坐标为2，求切点坐标与切线方程．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：先求导函数，设切点为（m，2），则由切线与直线y=-4x+3垂直，得2km=
，又km2=2，即可得到m，和切点，再由点斜式方程，即可得到切线方程．
| 1 |
| 4 |
解答：
解：由y=kx2，得y′=2kx，设切点为（m，2），
则km2=2①
由切线与直线y=-4x+3垂直，得2km=
②，
解之得m=16．
即切点坐标为（16，2），
切线方程为y-2=
（x-16）即为x-4y-8=0．
则km2=2①
由切线与直线y=-4x+3垂直，得2km=
| 1 |
| 4 |
解之得m=16．
即切点坐标为（16，2），
切线方程为y-2=
| 1 |
| 4 |
点评：利用导数研究函数的性质是导数的重要应用之一，导数的广泛应用为我们解决函数问题提供了有力的帮助．本小题主要考查利用导数求切点的坐标和切线方程．
练习册系列答案
相关题目
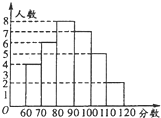某中学部分学生参加全国高中数学竞赛取得了优异成绩，指导老师统计了所有参赛同学的成绩（成绩都为整数，试题满分120分），并且绘制了“频数分布直方图”，请回答：