题目内容
已知函数f（x）=（sinx+cosx）2+2cos2x．
（1）求f（x）的最大值及最大值时自变量x的集合；
（2）求函数f（x）的单调增区间．
（1）求f（x）的最大值及最大值时自变量x的集合；
（2）求函数f（x）的单调增区间．
考点：两角和与差的正弦函数,正弦函数的单调性,三角函数的最值
专题：三角函数的求值,三角函数的图像与性质
分析：（1）利用二倍角公式以及两角和与差的三角函数化简函数为一个角的一个三角函数的形式，通过正弦函数的最值求f（x）的最大值及最大值时自变量x的集合；
（2）利用正弦函数的单调增区间，直接求函数f（x）的单调增区间．
（2）利用正弦函数的单调增区间，直接求函数f（x）的单调增区间．
解答：
解：（1）由题意得：f（x）=sin2x+2sinxcosx+cos2x+2cos2x
=sin2x+cos2x+2
=
sin(2x+
)+2…（4分）
所以当2x+
=2kπ+
(k∈Z)时，
即{x|x=kπ+
，k∈Z}…（6分）
f（x）取最大值，且f(x)max=2+
．…（7分）
（2）由2kπ-
≤2x+
≤2kπ+
，k∈Z，
得2kπ-
≤2x≤2kπ+
，k∈Z．所以kπ-
≤x≤kπ+
，k∈Z．
所以f（x）的单调递增区间为[kπ-
，kπ+
]，k∈Z…（10分）
=sin2x+cos2x+2
=
| 2 |
| π |
| 4 |
所以当2x+
| π |
| 4 |
| π |
| 2 |
即{x|x=kπ+
| π |
| 8 |
f（x）取最大值，且f(x)max=2+
| 2 |
（2）由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
得2kπ-
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 8 |
| π |
| 8 |
所以f（x）的单调递增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
点评：本题考查两角和与差的三角函数二倍角公式的应用，正弦函数的图象与性质，是中档题．
练习册系列答案
相关题目
已知函数f（x）=lg
，若f（a）=b（b≠0），则f（-a）等于（ ）
| 1-x |
| 1+x |
| A、-b | ||
| B、b | ||
C、
| ||
D、-
|
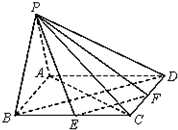如图，在四棱锥P-ABCD中，四边形ABCD是菱形，PB=PD，且EF分别是BC，CD的中点．求证：
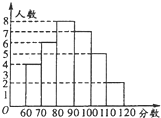某中学部分学生参加全国高中数学竞赛取得了优异成绩，指导老师统计了所有参赛同学的成绩（成绩都为整数，试题满分120分），并且绘制了“频数分布直方图”，请回答：