题目内容
12.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的一个焦点与抛物线${y^2}=4\sqrt{3}x$的焦点重合,长轴长等于圆x2+y2-2x-15=0的半径,则椭圆C的方程为( )| A. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C. | $\frac{x^2}{4}+{y^2}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |
分析 求出抛物线的焦点坐标,圆的半径,然后求解椭圆的a,b,即可得到椭圆方程.
解答 解:椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的一个焦点与抛物线${y^2}=4\sqrt{3}x$的焦点重合,可得c=$\sqrt{3}$,
长轴长等于圆x2+y2-2x-15=0的半径,a=2,则b=1,
所求椭圆方程为:$\frac{x^2}{4}+{y^2}=1$.
故选:C.
点评 本题考查椭圆的简单性质,椭圆方程的求法,抛物线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
2.设A,B是两个非空集合,定义集合A-B={x|x∈A且x∉B}.若A={x∈N|0≤x≤5},B={x|x2-7x+10<0},则A-B=( )
| A. | {0,1} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,5} |
3.下列命题推断错误的是( )
| A. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| B. | 若p且q为假命题,则p,q均为假命题 | |
| C. | “x=-1”是“x2-5x-6=0”的充分不必要条件 | |
| D. | 命题p:存在x0∈R,使得x02+x0+1<0,则非p:任意x∈R,都有x2+x+1≥0 |
20.在区间[-2,3]中任取一个数m,则使“双曲线$\frac{{x}^{2}}{{m}^{2}-1}$-$\frac{{y}^{2}}{4-m}$=1的离心率大于$\sqrt{3}$的概率是( )
| A. | $\frac{7}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
17.已知函数f(x)=log3|x-t|是偶函数,记$a=f({{{log}_{0.3}}4}),b=f({{π^{1.5}}}),c=f({2-t})$则a,b,c的大小关系为( )
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | c<b<a |
1.在投篮测试中,每人投3次,其中至少有两次投中才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学能通过测试的概率为( )
| A. | 0.352 | B. | 0.432 | C. | 0.36 | D. | 0.648 |
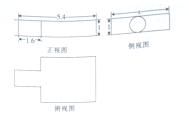 中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中x的为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中x的为( )