题目内容
4.数列{an}各项均为正数,且满足a1=1,$\sqrt{\frac{1}{a_n^2}+3}=\sqrt{\frac{1}{{a_{n+1}^2}}}$.记${b_n}=\frac{1}{{a_n^2a_{n+1}^2}}$,数列{bn}前n项的和为Sn,若Sn<t对任意的n∈N*恒成立,则实数t的取值范围是$[{\frac{1}{3},+∞})$.分析 满足a1=1,$\sqrt{\frac{1}{a_n^2}+3}=\sqrt{\frac{1}{{a_{n+1}^2}}}$.$\frac{1}{{a}_{n+1}^{2}}$-$\frac{1}{{a}_{n}^{2}}$=3,利用等差数列的通项公式可得$\frac{1}{{a}_{n}^{2}}$,${b_n}=\frac{1}{{a_n^2a_{n+1}^2}}$=$\frac{1}{(3n-2)(3n+1)}$=$\frac{1}{3}(\frac{1}{3n-2}-\frac{1}{3n+1})$,利用“裂项求和”方法与数列的单调性即可得出.
解答 解:∵满足a1=1,$\sqrt{\frac{1}{a_n^2}+3}=\sqrt{\frac{1}{{a_{n+1}^2}}}$.∴$\frac{1}{{a}_{n+1}^{2}}$-$\frac{1}{{a}_{n}^{2}}$=3,
∴数列$\{\frac{1}{{a}_{n}^{2}}\}$是等差数列,公差为3,首项为1.
∴$\frac{1}{{a}_{n}^{2}}$=1+3(n-1)=3n-2,
∴${b_n}=\frac{1}{{a_n^2a_{n+1}^2}}$=$\frac{1}{(3n-2)(3n+1)}$=$\frac{1}{3}(\frac{1}{3n-2}-\frac{1}{3n+1})$,
∴数列{bn}前n项的和为Sn=$\frac{1}{3}[(1-\frac{1}{4})$+$(\frac{1}{4}-\frac{1}{7})$+…+$(\frac{1}{3n-2}-\frac{1}{3n+1})]$
=$\frac{1}{3}(1-\frac{1}{3n+1})$,
若Sn<t对任意的n∈N*恒成立,∴$t≥\frac{1}{3}$.
则实数t的取值范围是$[{\frac{1}{3},+∞})$.
故答案为:$[{\frac{1}{3},+∞})$.
点评 本题考查了等差数列的通项公式、“裂项求和”方法、数列的单调性,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C. | $\frac{x^2}{4}+{y^2}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |
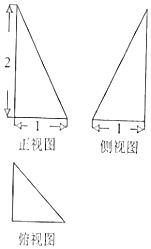
| A. | $\sqrt{6}π$ | B. | 6π | C. | 24π | D. | 36π |
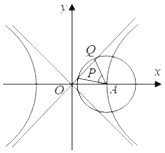 如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点为A,O 为坐标原点,以A 为圆心的圆与双曲线C 的一条渐近线交于 P,Q 两点.若∠PAQ=60°,且|PQ|=$\frac{{\sqrt{3}}}{3}a$,则双曲线C 的渐近线方程为( )
如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点为A,O 为坐标原点,以A 为圆心的圆与双曲线C 的一条渐近线交于 P,Q 两点.若∠PAQ=60°,且|PQ|=$\frac{{\sqrt{3}}}{3}a$,则双曲线C 的渐近线方程为( )| A. | $y=±\frac{{\sqrt{3}}}{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{2}x$ | C. | y=±3x | D. | $y=±\frac{{2\sqrt{3}}}{3}x$ |