题目内容
20.在区间[-2,3]中任取一个数m,则使“双曲线$\frac{{x}^{2}}{{m}^{2}-1}$-$\frac{{y}^{2}}{4-m}$=1的离心率大于$\sqrt{3}$的概率是( )| A. | $\frac{7}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
分析 双曲线$\frac{{x}^{2}}{{m}^{2}-1}$-$\frac{{y}^{2}}{4-m}$=1的离心率大于$\sqrt{3}$,则$\frac{{m}^{2}-1+4-m}{{m}^{2}-1}$>3,解得-2<m<-1,-1<m<1,1<m<$\frac{3}{2}$,可得区间长度,求出在区间[-2,3]上随机取一个实数m的区间长度,即可得出结论.
解答 解:因为双曲线$\frac{{x}^{2}}{{m}^{2}-1}$-$\frac{{y}^{2}}{4-m}$=1的离心率大于$\sqrt{3}$,则$\frac{{m}^{2}-1+4-m}{{m}^{2}-1}$>3,解得-m<-1,m>1,1<m<$\frac{3}{2}$,所求概率为$\frac{-1+2+\frac{3}{2}-1}{3+2}$=$\frac{3}{10}$.
故选B.
点评 本题考查了椭圆的方程以及几何概型的公式;属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
10.设公比为q(q>0)的等比数列{an}的前项和为Sn,若S2=3a2+2,S4=3a4+2,则a1=( )
| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
8.对于函数f(x)=atanx+bx3+cx(a、b、c∈R),选取a、b、c的一组值计算f(1)、f(-1),所得出的正确结果可能是( )
| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |
15.已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f(x)g′(x)>f′(x)g(x),f(x)=ax•g(x)(a>0,a≠1),$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$,在有穷数列$\{\frac{f(n)}{g(n)}\}$(n=1,2…10)中,任意取正整数k(1≤k≤10),则前k项和大于$\frac{15}{16}$的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的一个焦点与抛物线${y^2}=4\sqrt{3}x$的焦点重合,长轴长等于圆x2+y2-2x-15=0的半径,则椭圆C的方程为( )
| A. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C. | $\frac{x^2}{4}+{y^2}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{4}=1$ |
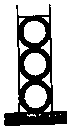 圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.
圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.