题目内容
已知A、B、C是△ABC的三内角,向量
=(-1,
),
=(cosA+1,sinA),且
⊥
.
(1)求角A;
(2)若
=-3,求tanC.
| m |
| 3 |
| n |
| m |
| n |
(1)求角A;
(2)若
| 1+sin2B |
| cos2B-sin2B |
考点:平面向量数量积的运算,同角三角函数基本关系的运用
专题:解三角形,平面向量及应用
分析:(1)利用数量积运算性质、两角和差正弦公式、正弦函数的单调性即可得出;
(2)利用同角三角函数基本关系式、两角和差的正切公式即可得出.
(2)利用同角三角函数基本关系式、两角和差的正切公式即可得出.
解答:
解:(1)∵
⊥
,∴
•
=0.
∴-(cosA+1)+
sinA=0,化为2sin(A-
)=1,
∴sin(A-
)=
.
∵0<A<π,∴-
≠A-
<
,∴A-
=
,解得A=
.
(2)由
=-3,化为sin2B-sinBcosB-2cos2B=0,
∵cosB≠0,∴tan2B-tanB-2=0,
∴tanB=2或tanB=-1;
而tanB=-1使cos2B-sin2B=0,故应舍去
,∴tanB=2,
∴tanC=-tan(A+B)=-
=
=
.
| m |
| n |
| m |
| n |
∴-(cosA+1)+
| 3 |
| π |
| 6 |
∴sin(A-
| π |
| 6 |
| 1 |
| 2 |
∵0<A<π,∴-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
(2)由
| 1+sin2B |
| cos2B-sin2B |
∵cosB≠0,∴tan2B-tanB-2=0,
∴tanB=2或tanB=-1;
而tanB=-1使cos2B-sin2B=0,故应舍去
,∴tanB=2,
∴tanC=-tan(A+B)=-
| tanA+tanB |
| 1-tanAtanB |
2+
| ||
1-2
|
8+5
| ||
| 11 |
点评:本题考查了数量积运算性质、两角和差正弦公式、正弦函数的单调性、同角三角函数基本关系式、两角和差的正切公式、诱导公式,考查了推理能力和计算能力,属于较难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
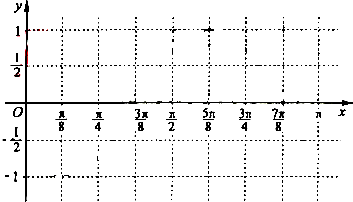 已知函数f(x)=sin2x+2sin(
已知函数f(x)=sin2x+2sin(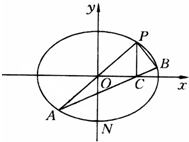 如图,在平面直角坐标系xOy中,过坐标原点的直线交椭圆
如图,在平面直角坐标系xOy中,过坐标原点的直线交椭圆