题目内容
已知函数f（x）=
（x∈R）是奇函数
（1）求实数a的值；
（2）判断并证明函数f（x）的单调性．
| a•2x+a-2 |
| 2x+1 |
（1）求实数a的值；
（2）判断并证明函数f（x）的单调性．
考点：函数奇偶性的性质,函数单调性的判断与证明
专题：函数的性质及应用
分析：（1）首先，根据函数为奇函数，f（0）=0，可以求解实数a的值；
（2）利用单调性的定义直接进行证明即可．
（2）利用单调性的定义直接进行证明即可．
解答：
解：（1）∵函数为奇函数，
∴f（0）=0，
即
=
=a-1=0，
解得a=1，
∴a=1．
（2）根据（1），得
函数f（x）=
=
=1-
，
它在R上为单调增函数．证明如下：
任设x1，x2?R，x1＜x2，
∵f（x1）-f（x2）=1-
-1+
=
∵x1＜x2，
∴2x1-2x2＜0，
∴f（x1）-f（x2）＜0，
∴函数f（x）在R上为单调增函数．
∴f（0）=0，
即
| a•20+a-2 |
| 20+1 |
| 2a-2 |
| 2 |
解得a=1，
∴a=1．
（2）根据（1），得
函数f（x）=
| 2x-1 |
| 2x+1 |
| 2x+1-2 |
| 2x+1 |
| 2 |
| 2x+1 |
它在R上为单调增函数．证明如下：
任设x1，x2?R，x1＜x2，
∵f（x1）-f（x2）=1-
| 2 |
| 2x1+1 |
| 2 |
| 2x2+1 |
=
| 2(2x1-2x2) |
| (2x1+1)(2x2+1) |
∵x1＜x2，
∴2x1-2x2＜0，
∴f（x1）-f（x2）＜0，
∴函数f（x）在R上为单调增函数．
点评：本题重点考查了函数的奇偶性和单调性，利用单调性的定义证明问题时，一定要分解到足以判断符号为止，切不可随意判断符合，导致不该出现的错误．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
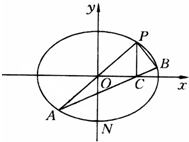如图，在平面直角坐标系xOy中，过坐标原点的直线交椭圆
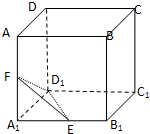如图，在正方体ABCD-A1B1C1D1中，E，F分别为棱A1B1，A1A的中点．