题目内容
8.设O为△ABC的外心,且5$\overrightarrow{OA}+12\overrightarrow{OB}+13\overrightarrow{OC}=\overrightarrow{0}$,则△ABC的内角C的值为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 设出外接圆的半径,由5$\overrightarrow{OA}+12\overrightarrow{OB}+13\overrightarrow{OC}=\overrightarrow{0}$,移项得$5\overrightarrow{OA}+12\overrightarrow{OB}=-13\overrightarrow{OC}$,再平方得到$\overrightarrow{OA}$•$\overrightarrow{OB}$,从而得到∠AOB,最后根据圆心角等于同弧所对的圆周角的两倍得△ABC中的内角C值.
解答 解:设外接圆的半径为R,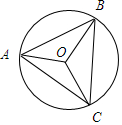
∵5$\overrightarrow{OA}+12\overrightarrow{OB}+13\overrightarrow{OC}=\overrightarrow{0}$,
∴移项得$5\overrightarrow{OA}+12\overrightarrow{OB}=-13\overrightarrow{OC}$,
∴($5\overrightarrow{OA}+12\overrightarrow{OB}$)2=(-13$\overrightarrow{OC}$)2,
∴169R2+120$\overrightarrow{OA}•\overrightarrow{OB}$=169R2,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,∴∠AOB=$\frac{π}{2}$,
∵根据圆心角等于同弧所对的圆周角的关系如图:
所以△ABC中的内角C值为$\frac{π}{4}$.
故选:C.
点评 本小题主要考查三角形外心的应用、向量在几何中的应用等基础知识,考查运算求解能力与转化思想.属于中档题.

| A. | 56 | B. | 60 | C. | 64 | D. | 68 |
| A. | 3 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
 2016年入冬以来,各地雾霾天气频发,PM2.5频频爆表(PM2.5是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与PM2.5的浓度是否相关,某市现采集到周一到周五某一时间段车流量与PM2.5的数据如表:
2016年入冬以来,各地雾霾天气频发,PM2.5频频爆表(PM2.5是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与PM2.5的浓度是否相关,某市现采集到周一到周五某一时间段车流量与PM2.5的数据如表:| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(2)试判断x与y是否具有线性关系,若有请求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,若没有,请说明理由
参考公式:
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.