题目内容
已知F1F2是椭圆
+
=1(a>b>0)的左、右两个焦点,A是椭圆上一点,△AF1F2的周长为10,椭圆的离心率为
.
(1)求椭圆的方程;
(2)若弦AB过右焦点F2交椭圆于B,且△F1AB的面积为5,求弦AB的直线方程.
| x2 |
| 9 |
| y2 |
| 5 |
| 2 |
| 3 |
(1)求椭圆的方程;
(2)若弦AB过右焦点F2交椭圆于B,且△F1AB的面积为5,求弦AB的直线方程.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用△AF1F2的周长为10,椭圆的离心率为
,求出几何量,即可求椭圆的方程;
(2)法㈠分类讨论,设直线方程与椭圆方程联立,求出面积,利用△F1AB的面积为5,即可求弦AB的直线方程;法㈡:设直线AB方程为x=ty+2与椭圆方程联立,求出面积,利用△F1AB的面积为5,即可求弦AB的直线方程.
| 2 |
| 3 |
(2)法㈠分类讨论,设直线方程与椭圆方程联立,求出面积,利用△F1AB的面积为5,即可求弦AB的直线方程;法㈡:设直线AB方程为x=ty+2与椭圆方程联立,求出面积,利用△F1AB的面积为5,即可求弦AB的直线方程.
解答:
解:(1)由题意知:
,
解得a=3,c=2,∴b=
.
∴椭圆方程为
+
=1…(5分)
(2)法㈠当直线AB的斜率不存在时,直线AB的方程为x=2
联立解得:A(2,
),B(2,-
),
∴|AB|=
,
∴S△F1AB=
|F1F2|•|AB|=
•4•
=
不合题意,舍去.
当直线AB的斜率存在时,设直线AB的方程为y=k(x-2),
,联立(9k2+5)y2+20ky-25k2=0,
设A(x1,y1),B(x2,y2),由韦达定理得:y1+y2=-
,y1•y2=
.…(8分)S△F1AB=S△F1F2A+S△F1F2B=
|F1F2|•|y1|+
|F1F2|•|y2|=
2c•|y1-y2|=5
∴|y1-y2|=
=
=
=10
,
∴63k4+54k2-25=0,∴k2=
,k2=-
(舍去),∴k=±
,
∴弦AB所在的直线方程x-
y-2=0或x+
y-2=0.…(12分)
法㈡:设直线AB方程为x=ty+2(t∈R),
直线方程和椭圆方程联立
,
消去x,(9+5t2)y2+20ty-25=0设A(x1,y1),B(x2,y2),
由韦达定理得:y1+y2=
,y1•y2=
.…(7分)S△F1AB=S△F1F2A+S△F1F2B=
|F1F2|•|y1|+
|F1F2|•|y2|=
2c•|y1-y2|=5.
∴|y1-y2|=
=
=
=
=30
两边平方:25t4-54t2-63=0,
∴(25t2+21t2)(t2-3)=0,∴t=±
.
∴弦AB所在的直线方程x-
y-2=0或x+
y-2=0.…(12分)
|
解得a=3,c=2,∴b=
| 5 |
∴椭圆方程为
| x2 |
| 9 |
| y2 |
| 5 |
(2)法㈠当直线AB的斜率不存在时,直线AB的方程为x=2
|
联立解得:A(2,
| 5 |
| 3 |
| 5 |
| 3 |
∴|AB|=
| 10 |
| 3 |
∴S△F1AB=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
| 20 |
| 3 |
当直线AB的斜率存在时,设直线AB的方程为y=k(x-2),
|
设A(x1,y1),B(x2,y2),由韦达定理得:y1+y2=-
| 20k |
| 9k2+5 |
| -25k2 |
| 9k2+5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴|y1-y2|=
| 5 |
| 2 |
| (y1+y2)2-4y1•y2 |
| 5 |
| 2 |
|
|
∴63k4+54k2-25=0,∴k2=
| 1 |
| 3 |
| 25 |
| 21 |
| ||
| 3 |
∴弦AB所在的直线方程x-
| 3 |
| 3 |
法㈡:设直线AB方程为x=ty+2(t∈R),
直线方程和椭圆方程联立
|
消去x,(9+5t2)y2+20ty-25=0设A(x1,y1),B(x2,y2),
由韦达定理得:y1+y2=
| -20t |
| 9+5t2 |
| -25 |
| 9+5t2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴|y1-y2|=
| 5 |
| 2 |
| (y1+y2)2-4y1•y2 |
=
|
|
| ||
| 9+5t2 |
两边平方:25t4-54t2-63=0,
∴(25t2+21t2)(t2-3)=0,∴t=±
| 3 |
∴弦AB所在的直线方程x-
| 3 |
| 3 |
点评:本题考查椭圆方程,考查直线与椭圆的位置关系,考查三角形面积的计算,正确运用韦达定理是关键.

练习册系列答案
相关题目
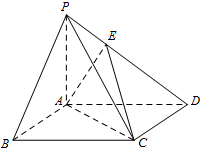 如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA=AB=2,PB=PD=2
如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA=AB=2,PB=PD=2