题目内容
设a>0且a∈Q,b=
.
(Ⅰ)证明:a≠b;
(Ⅱ)求证:在数轴上,
介于a与b之间,且距a较远;
(Ⅲ)在数轴上,a与b之间的距离是否可能为整数?若有,则求出这个整数;若没有,说明理由.
| a+2 |
| a+1 |
(Ⅰ)证明:a≠b;
(Ⅱ)求证:在数轴上,
| 2 |
(Ⅲ)在数轴上,a与b之间的距离是否可能为整数?若有,则求出这个整数;若没有,说明理由.
考点:不等式比较大小
专题:不等式的解法及应用
分析:(I)用反证法即可证明;
(II)利用已知只要证明(a-
)(b-
)<0,就可以证明在数轴上,
介于a与b之间.
当a<b,只要证明(
-a)-(b-
)>0;当a>b,只要证明(a-
)-(
-b)>0即可.
(III)使用反证法:假设存在整数m为a与b之间的距离,不妨设a-b=m,m=a-b=
,化为a2-2=m(a+1),利用求根公式解得a,只要证明不存在整数m满足a>0即可.
(II)利用已知只要证明(a-
| 2 |
| 2 |
| 2 |
当a<b,只要证明(
| 2 |
| 2 |
| 2 |
| 2 |
(III)使用反证法:假设存在整数m为a与b之间的距离,不妨设a-b=m,m=a-b=
| a2-2 |
| a+1 |
解答:
证明:(Ⅰ)假设b=a,则a=
,化为a2=2,解得a=±
,这与a>0且a∈Q相矛盾,
∴假设是错误的,
因此a≠b.
(Ⅱ)∵a>0且a∈Q,b=
.
∴(a-
)(b-
)=(a-
)(
-
)=-
<0,
∴
或
,
∴a<
<b或b<
<a.
∴在数轴上,
介于a与b之间.
若a<b,则(
-a)-(b-
)=2
-a-
=-
,
∵0<a<
,∴a-
<0,a-
+2>0,a+1>0.
∴(
-a)-(b-
)>0.
∴
距a较远;
当a>b时,同理可证明.
(Ⅲ)假设存在整数m为a与b之间的距离,不妨设a-b=m,
则m=a-b=a-
=
,∴a2-2=m(a+1),
化为a2-ma-m-2=0,解得a=
,
∵a∈Q,∴只有m=-2时满足,∴a=
,解得a=0或-2.这与a>0矛盾.
∴在数轴上,a与b之间的距离不可能为整数.
| a+2 |
| a+1 |
| 2 |
∴假设是错误的,
因此a≠b.
(Ⅱ)∵a>0且a∈Q,b=
| a+2 |
| a+1 |
∴(a-
| 2 |
| 2 |
| 2 |
| a+2 |
| a+1 |
| 2 |
(
| ||||
| a+1 |
∴
|
|
∴a<
| 2 |
| 2 |
∴在数轴上,
| 2 |
若a<b,则(
| 2 |
| 2 |
| 2 |
| a+2 |
| a+1 |
(a-
| ||||
| a+1 |
∵0<a<
| 2 |
| 2 |
| 2 |
∴(
| 2 |
| 2 |
∴
| 2 |
当a>b时,同理可证明.
(Ⅲ)假设存在整数m为a与b之间的距离,不妨设a-b=m,
则m=a-b=a-
| a+2 |
| a+1 |
| a2-2 |
| a+1 |
化为a2-ma-m-2=0,解得a=
m±
| ||
| 2 |
∵a∈Q,∴只有m=-2时满足,∴a=
| -2±2 |
| 2 |
∴在数轴上,a与b之间的距离不可能为整数.
点评:本题考查了反证法、一元二次不等式的解法、与实数(有理数)有关的问题,属于难题.

练习册系列答案
相关题目
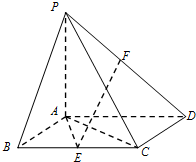 如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.