题目内容
已知函数f(x)=2x3+
x2-3x+2
(Ⅰ)求f(x)的单调区间.
(Ⅱ)求f(x)[-2,1]上的最大值和最小值.
| 3 |
| 2 |
(Ⅰ)求f(x)的单调区间.
(Ⅱ)求f(x)[-2,1]上的最大值和最小值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:综合题,导数的概念及应用
分析:(Ⅰ)求导数f'(x),解f'(x)>0可得增区间,解f'(x)<0可得减区间;
(Ⅱ)由(Ⅰ)求得f(x)的极值,再求f(-2),f(1),进行大小比较,其中最大者为最大值,最小者为最小值;
(Ⅱ)由(Ⅰ)求得f(x)的极值,再求f(-2),f(1),进行大小比较,其中最大者为最大值,最小者为最小值;
解答:
解:(Ⅰ)f(x)=2x3+
x2-3x+2,
f'(x)=6x2+3x-3,解f'(x)=0,得x=-1或x=
,
当x<-1或x>
时,f′(x)>0,f(x)递增;当-1<x<
时,f'(x)<0,f(x)递减;
∴f(x)的单调增区间为(-∞,-1)和(
,+∞),单调减区间为(-1,
);
(Ⅱ)由(Ⅰ)知,f(x)在[-2,-1]上递增,在[-1,
]上递减,在[
,1]上递增,
又f(-2)=-2,f(-1)=
,f(
)=
,f(1)=
,
∴f(x)的最大值为
,最小值为-2.
| 3 |
| 2 |
f'(x)=6x2+3x-3,解f'(x)=0,得x=-1或x=
| 1 |
| 2 |
当x<-1或x>
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)的单调增区间为(-∞,-1)和(
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)知,f(x)在[-2,-1]上递增,在[-1,
| 1 |
| 2 |
| 1 |
| 2 |
又f(-2)=-2,f(-1)=
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 8 |
| 5 |
| 2 |
∴f(x)的最大值为
| 9 |
| 2 |
点评:本题考查利用导数研究函数的单调性、求函数在闭区间上的最值,考查学生分析解决问题的能力,属中档题.正确理解导数与函数单调性间的关系是解题基础.

练习册系列答案
相关题目
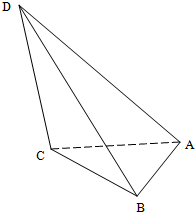 在四面体ABCD中,AB=AC=1,∠BAC=90°,AD=
在四面体ABCD中,AB=AC=1,∠BAC=90°,AD=