题目内容
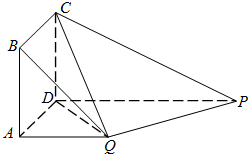 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面PDAQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面PDAQ,AB=AQ=| 1 |
| 2 |
(1)求证:棱锥Q-ABCCD与棱锥P-DCQ的体积相等.
(2)求异面直线CP与BQ所成角的大小(结果用反三角函数值表示).
考点:异面直线及其所成的角,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离,空间角
分析:(1)利用体积的计算方法将本题中的体积计算出来即可得出结论;
(2)确定∠PCE为异面直线PC与BQ所成角,利用余弦定理,即可求出异面直线CP与BQ所成角的大小.
(2)确定∠PCE为异面直线PC与BQ所成角,利用余弦定理,即可求出异面直线CP与BQ所成角的大小.
解答:
 (1)证明:设AB=a,由题设,QA⊥AD,QA⊥CD,知AQ为棱锥Q-ABCD的高,
(1)证明:设AB=a,由题设,QA⊥AD,QA⊥CD,知AQ为棱锥Q-ABCD的高,
所以棱锥Q一ABCD的体积V1=
a3,
棱锥P-DCQ的体积V2=VC-DPQ=
•
•2a•a•a=
a3,
故棱锥Q-ABCD的体积与棱锥P-DCQ的体积相等;
(2)解:因为AB=AQ=
DP,取PD中点E,连结QE,CE
则QE∥BC,且QE=BC,故CE∥BQ,
所以∠PCE为异面直线PC与BQ所成角.…(2分)
设AB=a,则在△PCE中,EP=a,CE=
a,CP=
a,…(4分)
由余弦定理,cos∠PCE=
=
.…(7分)
所以,异面直线CP与BQ所成角的大小为arccos
. …(8分)
 (1)证明:设AB=a,由题设,QA⊥AD,QA⊥CD,知AQ为棱锥Q-ABCD的高,
(1)证明:设AB=a,由题设,QA⊥AD,QA⊥CD,知AQ为棱锥Q-ABCD的高,所以棱锥Q一ABCD的体积V1=
| 1 |
| 3 |
棱锥P-DCQ的体积V2=VC-DPQ=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
故棱锥Q-ABCD的体积与棱锥P-DCQ的体积相等;
(2)解:因为AB=AQ=
| 1 |
| 2 |
则QE∥BC,且QE=BC,故CE∥BQ,
所以∠PCE为异面直线PC与BQ所成角.…(2分)
设AB=a,则在△PCE中,EP=a,CE=
| 2 |
| 5 |
由余弦定理,cos∠PCE=
| 2a2+5a2-a2 | ||||
2
|
3
| ||
| 10 |
所以,异面直线CP与BQ所成角的大小为arccos
3
| ||
| 10 |
点评:本题考查体积的计算,考查异面直线所成角,考查余弦定理,正确作出异面直线所成角是关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知角α的终边经过点P0(-3,-4),则cosα的值为( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
各项为正数的等比数列{an},a4•a7=2,则a1a2a3…a10的值为( )
| A、16 | B、32 | C、64 | D、128 |