题目内容
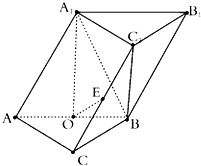 三棱柱ABC-A1B1C1,平面A1ABB1⊥平面ABC,AA1=AB=2,∠A1AB=60°,AC=BC=
三棱柱ABC-A1B1C1,平面A1ABB1⊥平面ABC,AA1=AB=2,∠A1AB=60°,AC=BC=| 2 |
(Ⅰ)求证:OE∥平面A1C1B;
(Ⅱ)求三棱锥B-A1AC的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明平面OEF∥平面A1C1B,可得OE∥平面A1C1B;
(Ⅱ)证明A1O⊥平面ABC,可得A1O是A1到平面ABC的距离,即可求三棱锥B-A1AC的体积.
(Ⅱ)证明A1O⊥平面ABC,可得A1O是A1到平面ABC的距离,即可求三棱锥B-A1AC的体积.
解答:
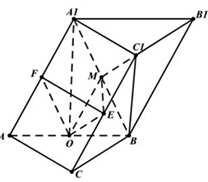 (Ⅰ)证明:取AA1的中点,连接OF,EF,
(Ⅰ)证明:取AA1的中点,连接OF,EF,
∵O,E分别是AB,CC1中点,
∴OF∥AB,
∵OF?平面A1C1B,AB?平面A1C1B,
∴OF∥平面A1C1B,
∵EF∥A1C1,
EF?平面A1C1B,AC?平面A1C1B,
∴EF∥平面A1C1B,
∵OF∩EF=F,
∴平面OEF∥平面A1C1B,
∴OE∥平面A1C1B;
(Ⅱ)解:∵平面A1ABB1⊥平面ABC,平面A1ABB1∩平面ABC=AB,A1O⊥平面ABC,
∴A1O⊥平面ABC,
∴A1O是A1到平面ABC的距离,
∵AC=BC=
,AB=2,
∴三棱锥B-A1AC的体积等于VA1-ABC=
•
•(
)2•
=
.
 (Ⅰ)证明:取AA1的中点,连接OF,EF,
(Ⅰ)证明:取AA1的中点,连接OF,EF,∵O,E分别是AB,CC1中点,
∴OF∥AB,
∵OF?平面A1C1B,AB?平面A1C1B,
∴OF∥平面A1C1B,
∵EF∥A1C1,
EF?平面A1C1B,AC?平面A1C1B,
∴EF∥平面A1C1B,
∵OF∩EF=F,
∴平面OEF∥平面A1C1B,
∴OE∥平面A1C1B;
(Ⅱ)解:∵平面A1ABB1⊥平面ABC,平面A1ABB1∩平面ABC=AB,A1O⊥平面ABC,
∴A1O⊥平面ABC,
∴A1O是A1到平面ABC的距离,
∵AC=BC=
| 2 |
∴三棱锥B-A1AC的体积等于VA1-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 3 |
点评:本题考查面面平行、线面平行,考查三棱锥B-A1AC的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
各项为正数的等比数列{an},a4•a7=2,则a1a2a3…a10的值为( )
| A、16 | B、32 | C、64 | D、128 |