题目内容
函数y=cos2（x+
）-sin2（x+
）是周期为 的 （填“奇”或“偶”）函数．
| π |
| 4 |
| π |
| 4 |
考点：二倍角的余弦
专题：三角函数的求值
分析：利用倍角公式可得函数y=cos2（x+
）-sin2（x+
）=cos(2x+
)=-2sin2x，即可得出．
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
解答：
解：函数y=cos2（x+
）-sin2（x+
）=cos(2x+
)=-2sin2x是周期为π的奇函数．
故答案为：π，奇．
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
故答案为：π，奇．
点评：本题考查了倍角公式的应用、函数周期性奇偶性，属于基础题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
已知复合命题p∧（￢q）是真命题，则下列命题中也是真命题的是（ ）
| A、（￢p）∨q |
| B、p∨q |
| C、p∧q |
| D、（￢p）∧（￢q） |
已知命题P：“若x≥a2+b2，则x≥2ab”，则下列说法正确的是（ ）
| A、命题P的逆命题是“若x＜a2+b2，则x＜2ab” |
| B、命题P的逆命题是“若x＜2ab，则x＜a2+b2” |
| C、命题P的否命题是“若x＜a2+b2，则x＜2ab” |
| D、命题P的否命题是“若x≥a2+b2，则x＜2ab” |
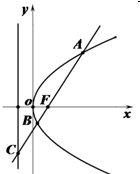如图，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=3|BF|，且|AF|=6，则此抛物线的方程为
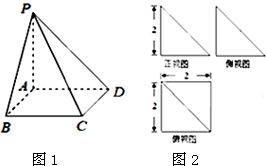已知四棱锥P-ABCD如图1所示，其三视图如图2所示，其中正视图和侧视图都是直角三角形，俯视图是矩形．其中E是PD的中点．