题目内容
已知等比数列{bn}的公比为3,数列{an}满足bn=3 an,n∈N*,且a1=1.
(1)判断{an}是何种数列,并给出证明;
(2)若Cn=
,Tn是数列{Cn}的前n项和,求使得Tn<
对所有n∈N*都成立的最小m.
(1)判断{an}是何种数列,并给出证明;
(2)若Cn=
| 1 |
| anan+1 |
| m |
| 30 |
考点:数列的求和,等差关系的确定,等比关系的确定
专题:等差数列与等比数列
分析:(1){an}是首项为1,公差为1的等差数列.bn=3an=3n,从而an=n,由此得到{an}是首项为1,公差为1的等差数列.
(2)由cn=
=
=
-
,利用裂项求和法有求出使得Tn<
对所有n∈N*都成立的最小m值为30.
(2)由cn=
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| m |
| 30 |
解答:
解:(1){an}是首项为1,公差为1的等差数列.
证明如下:
等比数列{bn}的公比为3,数列{an}满足bn=3 an,n∈N*,且a1=1.
∴b1=3a1=3,
b2=3a2=32,∴a2=2,
bn=3an=3n,∴an=n,
∴an+1-an=n+1-n=1,
∴{an}是首项为1,公差为1的等差数列.
(2)∵cn=
=
=
-
,
∴Tn=1-
+
-
+…+
-
=1-
<1,
∵Tn<
对所有n∈N*都成立,
∴
≥1,解得m≥30.
∴使得Tn<
对所有n∈N*都成立的最小m值为30.
证明如下:
等比数列{bn}的公比为3,数列{an}满足bn=3 an,n∈N*,且a1=1.
∴b1=3a1=3,
b2=3a2=32,∴a2=2,
bn=3an=3n,∴an=n,
∴an+1-an=n+1-n=1,
∴{an}是首项为1,公差为1的等差数列.
(2)∵cn=
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
∵Tn<
| m |
| 30 |
∴
| m |
| 30 |
∴使得Tn<
| m |
| 30 |
点评:本题考查数列是等差数列还是等比数列的判断与证明,考查满足条件的实数值的最小值的求法,解题时要注意裂项求和法的合理运用.

练习册系列答案
相关题目
已知命题P:“若x≥a2+b2,则x≥2ab”,则下列说法正确的是( )
| A、命题P的逆命题是“若x<a2+b2,则x<2ab” |
| B、命题P的逆命题是“若x<2ab,则x<a2+b2” |
| C、命题P的否命题是“若x<a2+b2,则x<2ab” |
| D、命题P的否命题是“若x≥a2+b2,则x<2ab” |




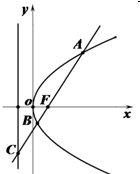 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=3|BF|,且|AF|=6,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=3|BF|,且|AF|=6,则此抛物线的方程为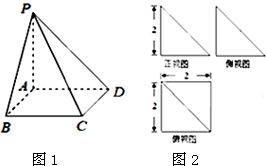 已知四棱锥P-ABCD如图1所示,其三视图如图2所示,其中正视图和侧视图都是直角三角形,俯视图是矩形.其中E是PD的中点.
已知四棱锥P-ABCD如图1所示,其三视图如图2所示,其中正视图和侧视图都是直角三角形,俯视图是矩形.其中E是PD的中点.