题目内容
如图，三个正方形并排放置，则∠BAE+∠CAD=（ ）
A、
| ||
B、
| ||
| C、75° | ||
| D、以上都不对 |
考点：两角和与差的正切函数
专题：计算题,三角函数的求值
分析：由图知，tan∠BAE=
，tan∠CAD=
，利用两角和的正切即可求得tan（∠BAE+∠CAD）的值，从而可得答案．
| 1 |
| 2 |
| 1 |
| 3 |
解答：
解：由图知，tan∠BAE=
，tan∠CAD=
，
∴tan（∠BAE+∠CAD）=
=
=1，又∠BAE与∠CAD均为锐角，
∴∠BAE+∠CAD=
．
故选：B．
| 1 |
| 2 |
| 1 |
| 3 |
∴tan（∠BAE+∠CAD）=
| tan∠BAE+tan∠CAD |
| 1-tan∠BAE•tan∠CAD |
| ||||
1-
|
∴∠BAE+∠CAD=
| π |
| 4 |
故选：B．
点评：本题考查两角和与差的正切函数，考查运算求解能力，属于中档题．
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
下列命题中正确的是（ ）
A、当x＞0且x≠1时，lgx+
| ||||||
B、当x＞0，
| ||||||
C、当0＜θ＜
| ||||||
D、当0＜x≤2时，x-
|
过两点A（4，y），B（2，-3）的直线的倾斜角是135°，则y=（ ）
| A、5 | B、-5 | C、1 | D、-1 |
下列命题中正确的是（ ）
A、“cosα=
| ||||
| B、函数y=f（x）在区间（a，b）内有零点，则f（a）•f（b）＜0 | ||||
| C、数列{an}是等比数列的充要条件是an+12=anan+2(n∈N*) | ||||
| D、命题“?x∈R，2x＞0”的否定是“?x∈R，2x≤0”． |
已知集合M={x|x2+2x-8＞0}，N=[2，3），则（ ）
| A、M⊆N |
| B、N⊆M |
| C、M∩N=（2，3） |
| D、M∪N=（-4，3） |
y=-3与y=sin3x的交点个数是（ ）
| A、0 | B、1 | C、2 | D、无数个 |
在△ABC中，若sinAcosB=cosAsinB，则△ABC为（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
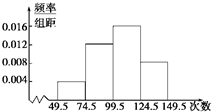春暖花开季节，某校举行了踢毽子比赛，将所得数据整理后，画出频率分布直方图如图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数为5．