题目内容
4．已知f（x）为定义在R上的奇函数，且当x≥0时，f（x）=x2-（a+4）x+a．（1）求实数a的值及f（x）的解析式；
（2）求使得f（x）=x+6成立的x的值．
分析 （1）根据函数的奇偶性得到f（0）=0，求出a的值即可；令-x＞0，得到x＜0，根据函数的奇偶性求出函数的解析式即可；
（2）根据函数解析式，建立方程，即可得出结论．
解答 解：（1）∵f（x）为定义在R上的奇函数，
∴f（0）=a=0，
由题意x≥0时：f（x）=x2-4x，
设x＜0，则-x＞0，
则f（-x）=x2+4x=-f（x），
故x＜0时，f（x）=-x2-4x，
故f（x）=$\left\{\begin{array}{l}{{x}^{2}-4x，x≥0}\\{-{x}^{2}-4x，x＜0}\end{array}\right.$．
（2）当x≥0时，x2-4x=x+6，可得x=6；
x＜0时，f（x）=-x2-4x=x+6，可得x=-2或-3．
综上所述，方程的解为6，-2或-3．
点评 本题考查了函数的奇偶性问题，考查求函数的解析式，是一道基础题．
练习册系列答案
53天天练系列答案
相关题目
15．已知函数$f（x）=1+x-\frac{x^2}{2}+\frac{x^3}{3}-…+\frac{{{x^{2017}}}}{2017}$，设F（x）=f（x+4），且F（x）的零点均在区间（a，b）内，其中a，b∈Z，a＜b，则F（x）＞0的最小整数解为（ ）
| A． | -1 | B． | 0 | C． | -5 | D． | -4 |
12．要得到函数$y=sin（{3x-\frac{π}{6}}）$的图象，只需将函数y=cos3x的图象（ ）
| A． | 向右平移$\frac{2π}{9}$个单位 | B． | 向左平移$\frac{2π}{9}$个单位 | ||
| C． | 向右平移$\frac{2π}{3}$个单位 | D． | 向左平移$\frac{2π}{3}$个单位 |
16．
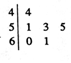为了检查某高三毕业班学生的体重情况，从该班随机抽取了6位学生进行称重，如图为6位学生体重的茎叶图（单位：kg），其中图中左边是体重的十位数字，右边是个位数字，则这6位学生体重的平均数为（ ）
为了检查某高三毕业班学生的体重情况，从该班随机抽取了6位学生进行称重，如图为6位学生体重的茎叶图（单位：kg），其中图中左边是体重的十位数字，右边是个位数字，则这6位学生体重的平均数为（ ）| A． | 52 | B． | 53 | C． | 54 | D． | 55 |
13．下列函数中是奇函数的是（ ）
| A． | y=x+sinx | B． | y=|x|-cosx | C． | y=xsinx | D． | y=|x|cosx |
14．下列各组中的函数f（x），g（x）表示同一函数的是（ ）
| A． | f（x）=x，g（x）=${（\sqrt{x}\;）^2}$ | B． | f（x）=x+1，g（x）=$\frac{{{x^2}-1}}{x-1}$ | ||
| C． | f（x）=|x|，g（x）=$\sqrt{{x}^{2}}$ | D． | f（x）=log22x，g（x）=2log2x |