已知正方形ABCD的边长为2.E为AB边的中点.则$\overrightarrow{ED}$•$\overrightarrow{EC}$=3．题目和参考答案——青夏教育精英家教网——

题目内容

19．已知正方形ABCD的边长为2，E为AB边的中点，则$\overrightarrow{ED}$•$\overrightarrow{EC}$=3．

分析以A为原点，以AB为x轴，AD为y轴建立平面直角坐标系，表示出对应点的坐标，求出$\overrightarrow{ED}$•$\overrightarrow{EC}$的值．

解答解：以A为原点，以AB为x轴，以AD为y轴建立直角坐标系，如图所示；

则O（0，0），B（2，0），C（2，2），D（0，2），E为AB的中点，
∴E（1，0）；
$\overrightarrow{ED}$=（-1，2），$\overrightarrow{EC}$=（1，2）；
∴$\overrightarrow{ED}$•$\overrightarrow{EC}$=-1×1+2×2=3．
故答案为：3．

点评本题考查了平面向量数量积的定义与应用问题，是基础题目．

练习册系列答案

全优点练课计划系列答案

单元双测全程提优测评卷系列答案

1课3练江苏人民出版社系列答案

尖子生新课堂课时作业系列答案

英才计划同步课时高效训练系列答案

金题1加1系列答案

100分闯关课时作业系列答案

学与练课时作业系列答案

优加学案课时通系列答案

1课1练系列答案

相关题目

9．观察下列各式：
C${\;}_{1}^{0}$=4⁰；
C${\;}_{3}^{0}$+C${\;}_{3}^{1}$=4¹；
C${\;}_{5}^{0}$+C${\;}_{5}^{1}$+C${\;}_{5}^{2}$=4²；
C${\;}_{7}^{0}$+C${\;}_{7}^{1}$+C${\;}_{7}^{2}$+C${\;}_{7}^{3}$=4³；
…
照此规律，当n∈N^*时，
C${\;}_{2n-1}^{0}$+C${\;}_{2n-1}^{1}$+C${\;}_{2n-1}^{2}$+…+C${\;}_{2n-1}^{n-1}$=（　　）

4ⁿ

4²ⁿ

10．若集合M⊆N，则以下集合中一定是空集的是（　　）

7．设矩阵M=$|\begin{array}{l}{m}&{2}\\{2}&{-3}\end{array}|$的一个特征值λ对应的特征向量为$[\begin{array}{l}{1}\\{-2}\end{array}]$，求m与λ的值．

14．已知函数$f（x）=\sqrt{a{x^2}+bx}$满足：对于实数a的某些值，可以找到相应正数b，使得f（x）的定义域与值域相同，那么符合条件的实数a的个数是2．

4．已知f（x）为定义在R上的奇函数，且当x≥0时，f（x）=x²-（a+4）x+a．
（1）求实数a的值及f（x）的解析式；
（2）求使得f（x）=x+6成立的x的值．

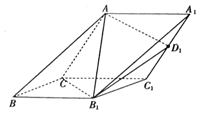如图，在三棱柱ABC-A₁B₁C₁中，侧面ACC₁A₁与侧面CBB₁C₁都是菱形，∠ACC₁=∠CC₁B₁=60°，AC=2$\sqrt{3}$．
（1）求证：AB₁⊥CC₁；
（2）若AB₁=3$\sqrt{2}$，A₁C₁的中点为D₁，求二面角C-AB₁-D₁的余弦值．

8．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右顶点分别是A₁，A₂，M是双曲线上任意一点，若直线MA₁，MA₂的斜率之积等于2，则该双曲线的离心率是$\sqrt{3}$．

9．已知A（2，3），B（4，-3），且$\overrightarrow{AP}$=3$\overrightarrow{AB}$，则点P的坐标为（8，-15）．