题目内容
已知函数f(x)=|x-a|+|x-1|,a∈R.
(1)当a=3时,解不等式f(x)≤4;
(2)当x∈(-2,1)时,f(x)>|2x-a-1|,求a的取值范围.
(1)当a=3时,解不等式f(x)≤4;
(2)当x∈(-2,1)时,f(x)>|2x-a-1|,求a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)当a=3时,f(x)=
,分类讨论求得它的解集.
(2)因为f(x)=|x-a|+|x-1|≥|x-a+x-1|=|2x-a-1|,分类讨论求得不等式(x-1)(x-a)<0的解集为A,再根据(-2,1)⊆A,求得a的取值范围.
|
(2)因为f(x)=|x-a|+|x-1|≥|x-a+x-1|=|2x-a-1|,分类讨论求得不等式(x-1)(x-a)<0的解集为A,再根据(-2,1)⊆A,求得a的取值范围.
解答:
解:(1)当a=3时,f(x)=
,
当x<1时,由f(x)≤4得4-2x≤4,解得0≤x<1;
当1≤x≤3时,f(x)≤4恒成立;
当x>3时,由f(x)≤4得2x-4≤4,解得3<x≤4,
所以不等式f(x)≤4的解集为{x|0≤x≤4}.
(2)因为f(x)=|x-a|+|x-1|≥|x-a+x-1|=|2x-a-1|,
当(x-1)(x-a)≥0时,f(x)=|2x-a-1|;
当(x-1)(x-a)<0时,f(x)>|2x-a-1|.…(7分)
记不等式(x-1)(x-a)<0的解集为A,则(-2,1)⊆A,
故a≤-2,所以a的取值范围是(-∞,-2].
|
当x<1时,由f(x)≤4得4-2x≤4,解得0≤x<1;
当1≤x≤3时,f(x)≤4恒成立;
当x>3时,由f(x)≤4得2x-4≤4,解得3<x≤4,
所以不等式f(x)≤4的解集为{x|0≤x≤4}.
(2)因为f(x)=|x-a|+|x-1|≥|x-a+x-1|=|2x-a-1|,
当(x-1)(x-a)≥0时,f(x)=|2x-a-1|;
当(x-1)(x-a)<0时,f(x)>|2x-a-1|.…(7分)
记不等式(x-1)(x-a)<0的解集为A,则(-2,1)⊆A,
故a≤-2,所以a的取值范围是(-∞,-2].
点评:本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
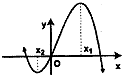 已知函数f(x)=ax3+bx2+x(a,b∈R,ab≠0)的图象如图所示(x1,x2为两个极值点),且|x1|>|x2|则有( )
已知函数f(x)=ax3+bx2+x(a,b∈R,ab≠0)的图象如图所示(x1,x2为两个极值点),且|x1|>|x2|则有( )| A、a>0,b>0 |
| B、a<0,b<0 |
| C、a<0,b>0 |
| D、a>0,b<0 |
使得(x+
)n(n∈N*)的展开式中含有常数项的最小的n是( )
| 1 | ||
x
|
| A、4 | B、5 | C、6 | D、7 |
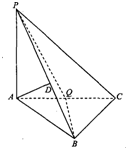 在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上,
在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上,