题目内容
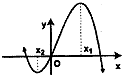已知函数f（x）=ax3+bx2+x（a，b∈R，ab≠0）的图象如图所示（x1，x2为两个极值点），且|x1|＞|x2|则有（ ）| A、a＞0，b＞0 |
| B、a＜0，b＜0 |
| C、a＜0，b＞0 |
| D、a＞0，b＜0 |
考点：利用导数研究函数的极值
专题：计算题,作图题,导数的综合应用
分析：由题意求导f′（x）=3ax2+2bx+1，则由x1，x2为两个极值点知x1，x2为3ax2+2bx+1=0的两个根，从而利用韦达定理求解．
解答：
解：由题意，f′（x）=3ax2+2bx+1；
则由x1，x2为两个极值点知，
x1，x2为3ax2+2bx+1=0的两个根，
则由图象可知，
x1x2=
＜0，x1+x2=-
＞0；
故a＜0，b＞0；
故选C．
则由x1，x2为两个极值点知，
x1，x2为3ax2+2bx+1=0的两个根，
则由图象可知，
x1x2=
| 1 |
| 3a |
| 2b |
| 3a |
故a＜0，b＞0；
故选C．
点评：本题考查了导数的综合应用及识图能力，属于中档题．
练习册系列答案
相关题目
下列问题不是解决问题的算法的是（ ）
| A、方程x2-4x+3=0有两个不等的实根 |
| B、解一元一次方程的步骤是去分母、去括号、移项、合并同类项、化系数为1 |
| C、从中山到北京先坐汽车，再坐火车 |
| D、解不等式ax+3＞0时，第一步移项，第二步讨论 |